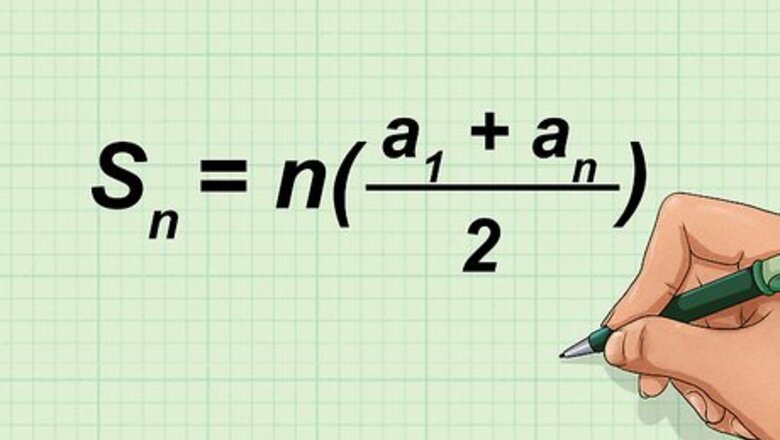
views
X
Research source
The basic method is pairing numbers in the group, then multiplying the sum of each pair by the number of pairs. From this method we can derive a formula for adding consecutive numbers
a
1
{\displaystyle a_{1}}
through
a
n
{\displaystyle a_{n}}
:
S
n
=
n
(
a
1
+
a
n
2
)
{\displaystyle S_{n}=n({\frac {a_{1}+a_{n}}{2}})}
. These methods can be applied to any series of consecutive numbers, not just 1 through 100.
Using the Formula for the Sum of a Series
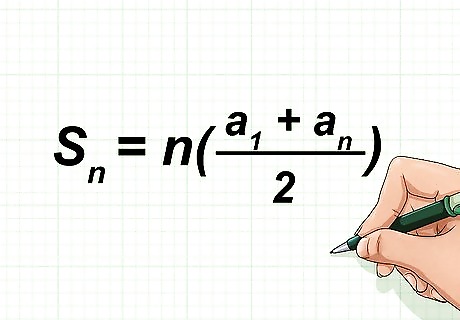
Write the formula for finding the sum of an arithmetic series. The formula is S n = n ( a 1 + a n 2 ) {\displaystyle S_{n}=n({\frac {a_{1}+a_{n}}{2}})} S_{{n}}=n({\frac {a_{{1}}+a_{{n}}}{2}}), where n {\displaystyle n} n equals the number of terms in the series, a 1 {\displaystyle a_{1}} a_{{1}} is the first number in the series, a n {\displaystyle a_{n}} a_{{n}} is the last number in the series, and S n {\displaystyle S_{n}} S_{{n}} equals the sum of n {\displaystyle n} n numbers.
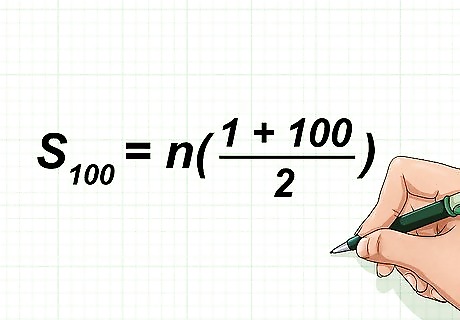
Plug the values into the formula. This means substituting the first term in the series for a 1 {\displaystyle a_{1}} a_{{1}}, and the last term in the series for a n {\displaystyle a_{n}} a_{{n}}. When adding consecutive numbers 1 through 100, a 1 = 1 {\displaystyle a_{1}=1} a_{{1}}=1 and a n = 100 {\displaystyle a_{n}=100} a_{{n}}=100. Thus, your formula will look like this: S 100 = n ( 1 + 100 2 ) {\displaystyle S_{100}=n({\frac {1+100}{2}})} S_{{100}}=n({\frac {1+100}{2}}).
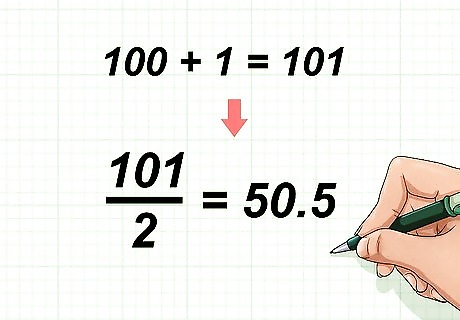
Add the values in the numerator of the fraction, then divide by 2. Since 100 + 1 = 101 {\displaystyle 100+1=101} 100+1=101, you will divide 101 by 2: 101 2 = 50.5 {\displaystyle {\frac {101}{2}}=50.5} {\frac {101}{2}}=50.5.
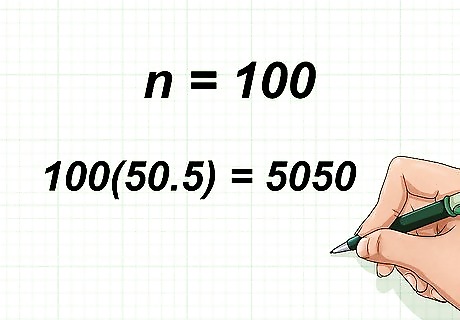
Multiply by n {\displaystyle n} n. This will give you the sum the consecutive number in the series. In this instance, since you are adding consecutive numbers to 100, n = 100 {\displaystyle n=100} n=100. So, you would calculate 100 ( 50.5 ) = 5050 {\displaystyle 100(50.5)=5050} 100(50.5)=5050. Thus, the sum of the consecutive numbers between 1 and 100 is 5,050. To quickly multiply a number by 100, move the decimal point two places to the right.
Using Gauss’s Technique

Divide the series into two equal groups. To find out how many numbers are in each group, divide the number of numbers by 2. In this instance, since the series is 1 to 100, you would calculate 100 ÷ 2 = 50 {\displaystyle 100\div 2=50} 100\div 2=50. So, the first group will have 50 numbers (1-50). The second group will also have 50 numbers (51-100).
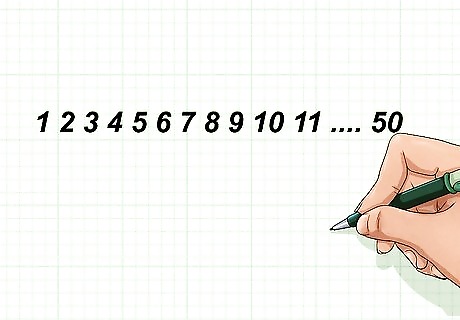
Write the first group, 1-50, in ascending order. Write the numbers in a row, beginning with 1 and ending with 50.
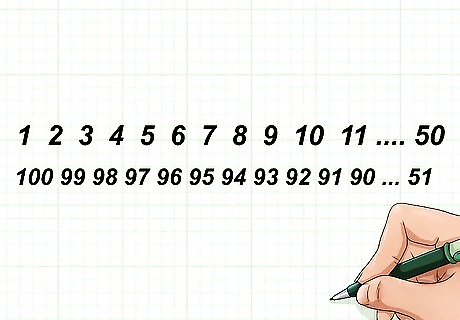
Write the second group, 100-51, in descending order. Write these numbers in a row under the first group. Begin so that 100 lines up under 1, 99 lines up under 2, etc.
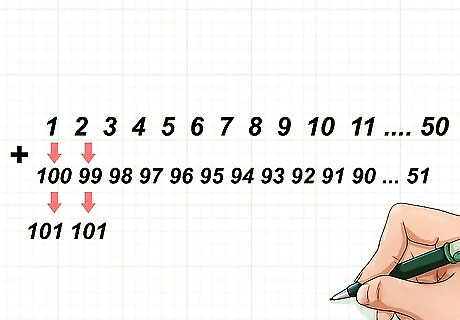
Add each vertical set of numbers. This means you will calculate 1 + 100 = 101 {\displaystyle 1+100=101} 1+100=101, 2 + 99 = 101 {\displaystyle 2+99=101} 2+99=101. etc. You don’t actually have to add up all the sets of numbers, because you should see that each set adds up to 101.
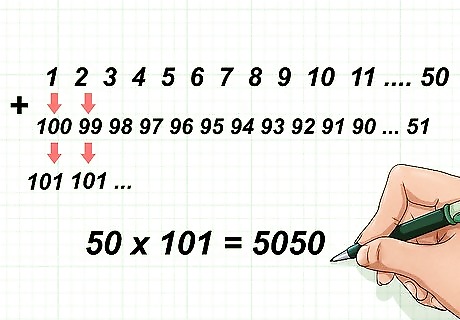
Multiply 101 times 50. To find the sum of consecutive numbers 1 to 100, you multiply the number of sets (50) by the sum of each set (101): 101 ( 50 ) = 5050. {\displaystyle 101(50)=5050.} 101(50)=5050. So, the sum of consecutive number 1 through 100 is 5,050.

















Comments
0 comment