How to Calculate Pi

Calculating Pi Using the Measurements of a Circle

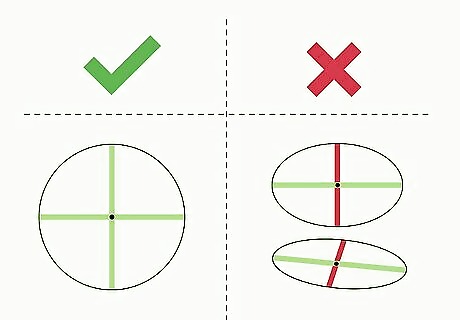
Make sure you are using a perfect circle. This method won't work with ellipses, ovals, or anything but a real circle. A circle is defined as all the points on a plane that are an equal distance from a single center point. The lids of jars are good household objects to use for this exercise. You should be able to calculate pi roughly because in order to get exact results of pi, you will need to have a very thin lead (or whatever you are using). Even the sharpest pencil graphite could be huge to have exact results.

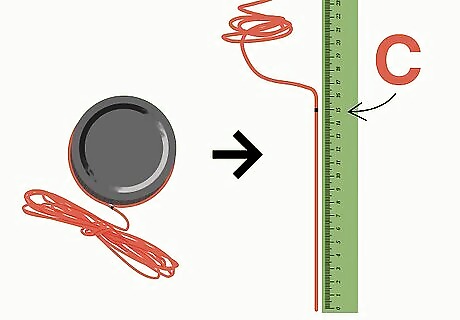
Measure the circumference of a circle as accurately as you can. The circumference is the length that goes around the entire edge of the circle. Since the circumference is round, it can be difficult to measure (that's why pi is so important). Lay a string over the circle as closely as you can. Mark the string off where it circles back around, and then measure the string length with a ruler.

Measure the diameter of the circle. The diameter runs from one side of the circle to the other through the circle's center point.

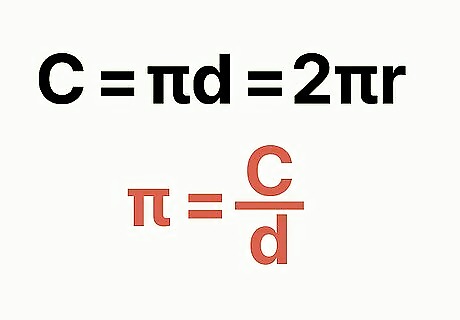
Use the formula. The circumference of a circle is found with the formula C=πd=2πr. Thus, pi equals a circle's circumference divided by its diameter. Plug your numbers into a calculator: the result should be roughly 3.14.

Repeat this process with several different circles, and then average the results. This will give you more accurate results. Your measurements might not be perfect on any given circle, but over time they should average out to a pretty accurate calculation of pi.

Calculating Pi Using an Infinite Series

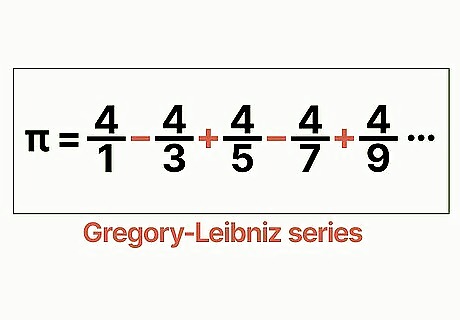
Use the Gregory-Leibniz series. Mathematicians have found several different mathematical series that, if carried out infinitely, will accurately calculate pi to a great number of decimal places. Some of these are so complex they require supercomputers to process them. One of the simplest, however, is the Gregory-Leibniz series. Though not very efficient, it will get closer and closer to pi with every iteration, accurately producing pi to five decimal places with 500,000 iterations. Here is the formula to apply. π=(4/1)-(4/3)+(4/5)-(4/7)+(4/9)-(4/11)+(4/13)-(4/15) ⋯ Take 4 and subtract 4 divided by 3. Then add 4 divided by 5. Then subtract 4 divided by 7. Continue alternating between adding and subtracting fractions with a numerator of 4 and a denominator of each subsequent odd number. The more times you do this, the closer you will get to pi.

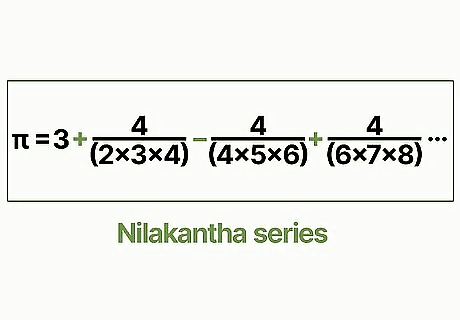
Try the Nilakantha series. This is another infinite series to calculate pi that is fairly easy to understand. While somewhat more complicated, it converges on pi much quicker than the Leibniz formula. π=3+4/(2·3·4)-4/(4·5·6)+4/(6·7·8)-4/(8·9·10)+4/(10·11·12)-4/(12·13·14) ⋯ For this formula, take three and start alternating between adding and subtracting fractions with numerators of 4 and denominators that are the product of three consecutive integers which increase with every new iteration. Each subsequent fraction begins its set of integers with the highest one used in the previous fraction. Carry this out even a few times and the results get fairly close to pi.

Calculating Pi Using a Limit

Pick a large number. The bigger the number, the more accurate your calculation will be.

Plug your number, which we'll call x, into this formula to calculate pi: x * sin(180 / x). For this to work, make sure your calculator is set to Degrees. The reason this is called a Limit is because the result of it is 'limited' to pi. As you increase your number x, the result will get closer and closer to the value of pi.

Using Arcsine Function/Inverse Sine Function

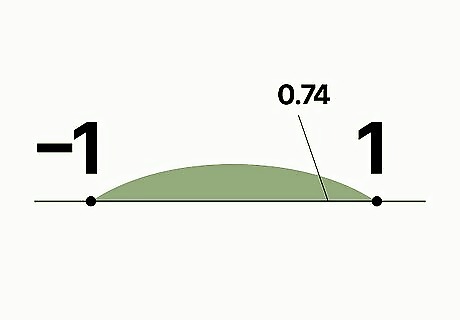
Pick any number between -1 and 1. This is because the Arcsin function is undefined for arguments greater than 1 or less than -1.

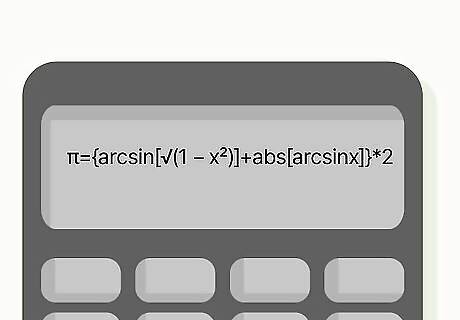
Plug your number into the following formula, and the result will be roughly equal to pi. π=｛arcsin[√(1 - x²)]+ abs[arcsin x]｝·2. Arcsin refers to the inverse sine in radians Sqrt is short for square root Abs is short for absolute value x^2 refers to an exponent, in this case, x squared.