How to Find the Least Common Multiple of Two Numbers

Listing all Multiples

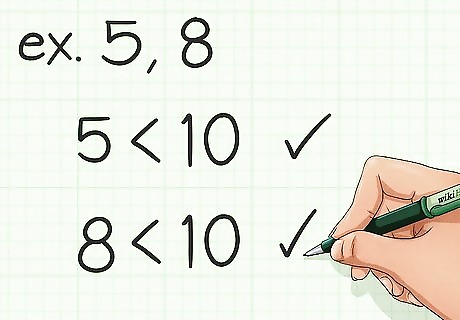
Assess your numbers. This method works best when you are working with two numbers that are less than 10. If you are working with larger numbers, it’s best to use a different method. For example, you might need to find the least common multiple of 5 and 8. Since these are small numbers, it is appropriate to use this method.

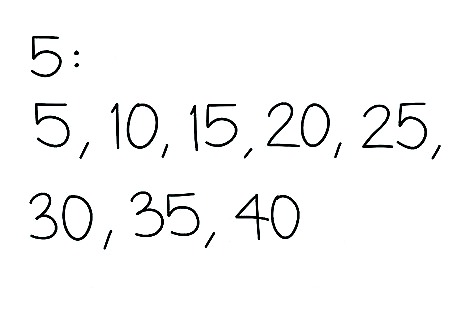
Write out the first several multiples of the first number. A multiple is a product of any number and an integer. In other words, they are the numbers you would see in a multiplication table. For example, the first several multiples of 5 are 5, 10, 15, 20, 25, 30, 35, and 40.

Write out the first several multiples of the second number. Do this near the first set of multiples, so that they are easy to compare. For example, the first several multiples of 8 are 8, 16, 24, 32, 40, 48, 56, and 64.

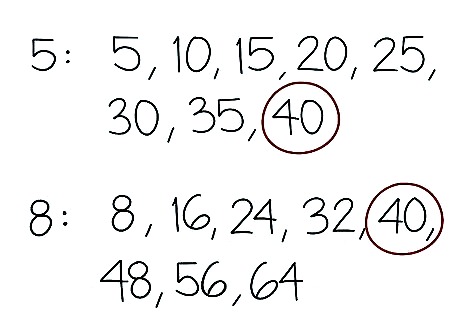
Find the smallest multiple the numbers have in common. You might need to extend your list of multiples until you find one both numbers share. This number will be your least common multiple. For example, the lowest multiple 5 and 8 share is 40, so the least common multiple of 5 and 8 is 40.

Using Prime Factorization

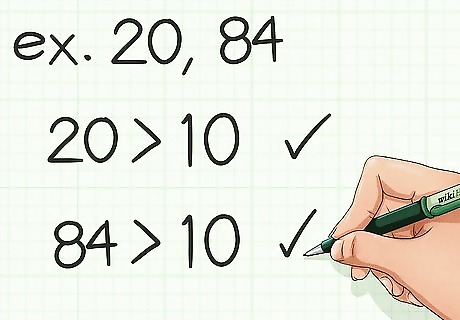
Assess your numbers. This method works best when both of the numbers you are working with are greater than 10. If you have smaller numbers, you can use a different method to find the least common multiple more quickly. For example, if you need to find the least common multiple of 20 and 84, you should use this method.

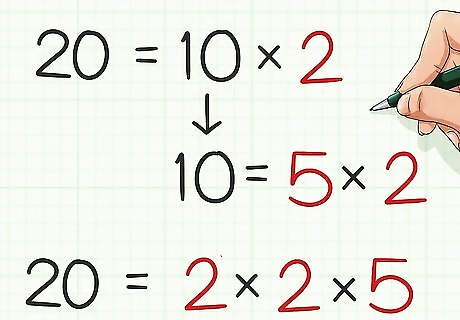
Factor the first number. You want to factor the number into its prime factors; that is, find the prime factors you can multiply together to get this number. One way to do this is by creating a factor tree. Once you are done factoring, rewrite the prime factors as an equation. For example, 2 × 10 = 20 {\displaystyle \mathbf {2} \times 10=20} {\mathbf {2}}\times 10=20 and 2 × 5 = 10 {\displaystyle \mathbf {2} \times \mathbf {5} =10} {\mathbf {2}}\times {\mathbf {5}}=10, so the prime factors of 20 are 2, 2, and 5. Rewriting as an equation, you get 20 = 2 × 2 × 5 {\displaystyle 20=2\times 2\times 5} 20=2\times 2\times 5.

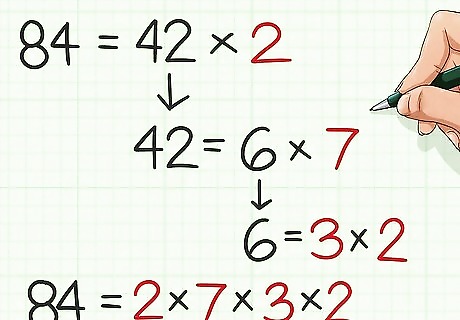
Factor the second number. Do this in the same way you factored the first number, finding the prime factors you can multiply together to get the number. For example, 2 × 42 = 84 {\displaystyle \mathbf {2} \times 42=84} {\mathbf {2}}\times 42=84, 7 × 6 = 42 {\displaystyle \mathbf {7} \times 6=42} {\mathbf {7}}\times 6=42, and 3 × 2 = 6 {\displaystyle \mathbf {3} \times \mathbf {2} =6} {\mathbf {3}}\times {\mathbf {2}}=6, so the prime factors of 84 are 2, 7, 3, and 2. Rewriting as an equation, you get 84 = 2 × 7 × 3 × 2 {\displaystyle 84=2\times 7\times 3\times 2} 84=2\times 7\times 3\times 2.

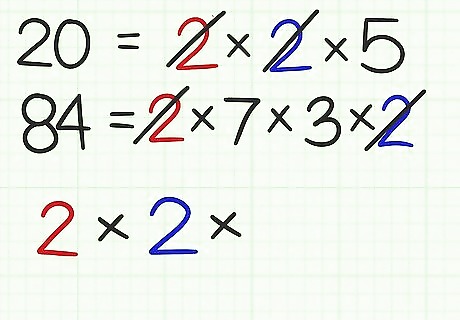
Write down the factors each number shares. Write the factors as a multiplication sentence. As you write each factor, cross it off in each numbers factorization equation. For example, both numbers share a factor of 2, so write 2 × {\displaystyle 2\times } 2\times and cross out a 2 in each number’s factorization equation. Each number also shares a second 2, so change the multiplication sentence to 2 × 2 {\displaystyle 2\times 2} 2\times 2 and cross out a second 2 in each factorization equation.

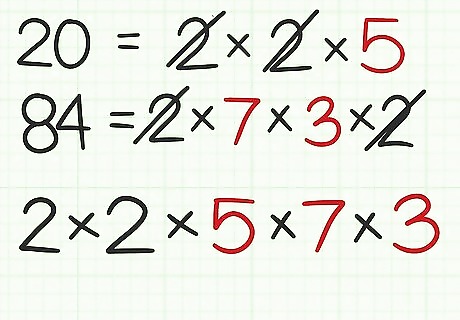
Add any leftover factors to the multiplication sentence. These are the factors you did not cross out when comparing the two groups of factors. Thus, these are factors that the two numbers do not share. For example, in the equation 20 = 2 × 2 × 5 {\displaystyle 20=2\times 2\times 5} 20=2\times 2\times 5, you crossed out both 2s, since these factors were shared with the other number. You have a factor of 5 left over, so add this to your multiplication sentence: 2 × 2 × 5 {\displaystyle 2\times 2\times 5} 2\times 2\times 5. In the equation 84 = 2 × 7 × 3 × 2 {\displaystyle 84=2\times 7\times 3\times 2} 84=2\times 7\times 3\times 2, you also crossed out both 2s. You have the factors 7 and 3 left over, so add these to your multiplication sentence: 2 × 2 × 5 × 7 × 3 {\displaystyle 2\times 2\times 5\times 7\times 3} 2\times 2\times 5\times 7\times 3.

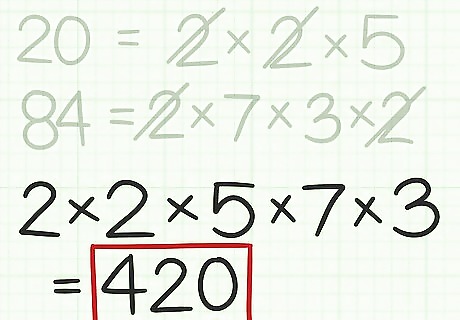
Calculate the least common multiple. To do this, multiply together all of the factors in your multiplication sentence. For example, 2 × 2 × 5 × 7 × 3 = 420 {\displaystyle 2\times 2\times 5\times 7\times 3=420} 2\times 2\times 5\times 7\times 3=420. So, the least common multiple of 20 and 84 is 420.

Using the Grid or Ladder Method

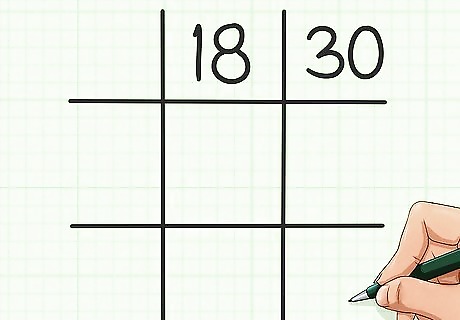
Draw a tic-tac-toe grid. A tic-tac-toe grid is two sets of parallel lines that intersect each other perpendicularly. The lines form three rows and three columns and looks like the pound key (#) on a phone or keyboard. Write your first number in the top-center square of the grid. Write your second number in the top-right square of the grid. For example, if you are trying to find the least common multiple of 18 and 30, write 18 in the top center of your grid, and 30 in the top right of your grid.

Look for a factor that is common to both numbers. Write this number in the top-left square of your grid. It is helpful to use prime factors, but you don’t necessarily have to. For example, since 18 and 30 are both even numbers, you know that that they both have a factor of 2. So write 2 in the top-left of the grid.

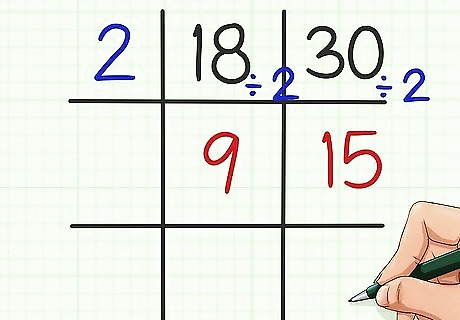
Divide the factor into each number. Write the quotient in the square below either number. A quotient is the answer to a division problem. For example, 18 ÷ 2 = 9 {\displaystyle 18\div 2=9} 18\div 2=9, so write 9 under 18 in the grid. 30 ÷ 2 = 15 {\displaystyle 30\div 2=15} 30\div 2=15, so write 15 under 30 in the grid.

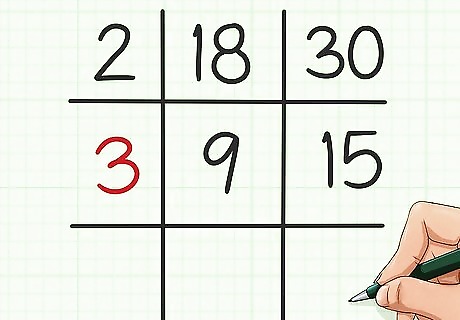
Find a factor that is common to the two quotients. If there is no factor common to both quotients, you can skip this and the next step. If there is a common factor, write it in the middle-left square of the grid. For example, 9 and 15 both have a factor of 3, so you would write 3 in the middle-left of the grid.

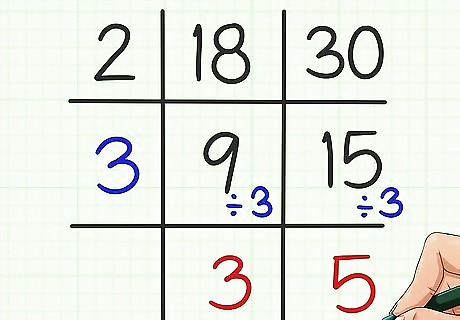
Divide this new factor into each quotient. Write this new quotient below the first ones. For example, 9 ÷ 3 = 3 {\displaystyle 9\div 3=3} 9\div 3=3, so write 3 under 9 in the grid. 15 ÷ 3 = 5 {\displaystyle 15\div 3=5} 15\div 3=5, so write 5 under 15 in the grid.

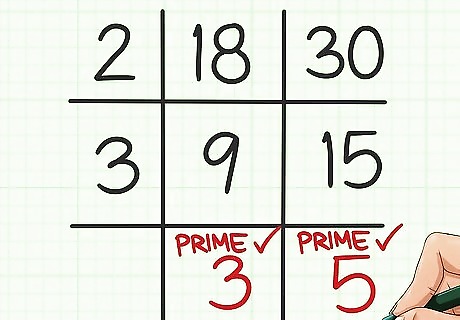
Extend your grid if necessary. Follow this same process until you reach a point where the last set of quotients have no common factor.

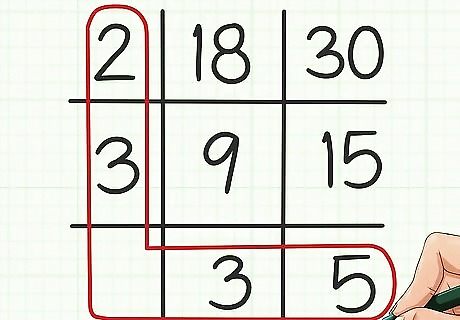
Draw a circle around the numbers in the first column and last row of your grid. You can think of it as drawing an “L” for “least common multiple.” Write a multiplication sentence using all of these factors. For example, since 2 and 3 are in the first column of the grid, and 3 and 5 are in the last row of the grid, you would write the sentence 2 × 3 × 3 × 5 {\displaystyle 2\times 3\times 3\times 5} 2\times 3\times 3\times 5.

Complete the multiplication. When you multiply all of these factors together, the result is the least common multiple of your two original numbers. For example, 2 × 3 × 3 × 5 = 90 {\displaystyle 2\times 3\times 3\times 5=90} 2\times 3\times 3\times 5=90. So, the least common multiple of 18 and 30 is 90.

Using Euclid’s Algorithm

Understand the vocabulary of division. The dividend is the number being divided. The divisor is the number the dividend is being divided by. The quotient is the answer to the division problem. The remainder is the amount left over after a number is divided by another. For example, in the equation 15 ÷ 6 = 2 remainder 3 {\displaystyle 15\div 6=2\;{\text{remainder}}\;3} 15\div 6=2\;{\text{remainder}}\;3:15 is the dividend6 is the divisor2 is the quotient3 is the remainder.

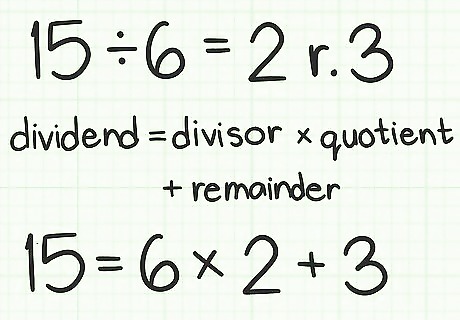
Set up the formula for the quotient-remainder form. The formula is dividend = divisor × quotient + remainder {\displaystyle {\text{dividend}}={\text{divisor}}\times {\text{quotient}}+{\text{remainder}}} {\text{dividend}}={\text{divisor}}\times {\text{quotient}}+{\text{remainder}}. You will use this form to set up Euclid’s algorithm to find the greatest common divisor of two numbers. For example, 15 = 6 × 2 + 3 {\displaystyle 15=6\times 2+3} 15=6\times 2+3. The greatest common divisor is the largest divisor, or factor, that two numbers share. In this method, you first find the greatest common divisor, and then use it to find the least common multiple.

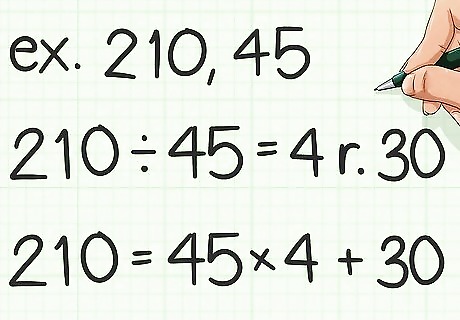
Use the larger of the two numbers as the dividend. Use the smaller of the two numbers as the divisor. Set up an equation in quotient-remainder form for these two numbers. For example, if you are trying to find the least common multiple of 210 and 45, you would calculate 210 = 45 × 4 + 30 {\displaystyle 210=45\times 4+30} 210=45\times 4+30.

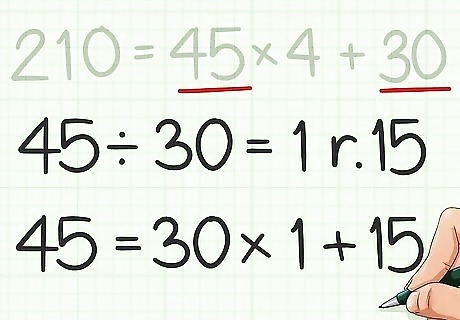
Use the original divisor as the new dividend. Use the remainder as the new divisor. Set up an equation in quotient-remainder form for these two numbers. For example, 45 = 30 × 1 + 15 {\displaystyle 45=30\times 1+15} {\displaystyle 45=30\times 1+15}.

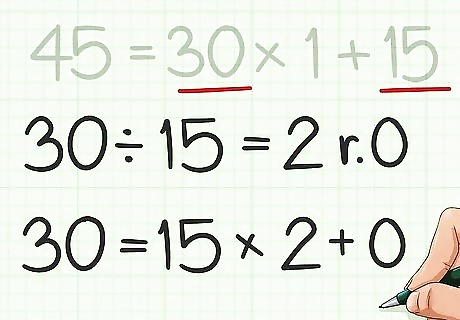
Repeat this process until you have a remainder of 0. For each new equation, use the previous equation’s divisor as the new dividend, and the previous remainder as the new divisor. For example, 30 = 15 × 2 + 0 {\displaystyle 30=15\times 2+0} 30=15\times 2+0. Since the remainder is 0, you do not need to divide any further.

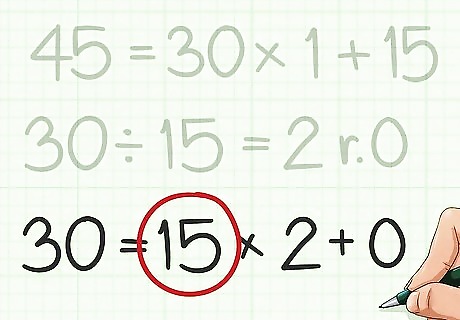
Look at the last divisor you used. This is the greatest common divisor for the two numbers. For example, since the last equation was 30 = 15 × 2 + 0 {\displaystyle 30=15\times 2+0} 30=15\times 2+0, the last divisor was 15, and so 15 is the greatest common divisor of 210 and 45.

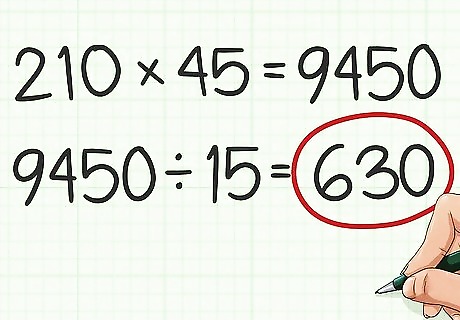
Multiply the two numbers. Divide the product by the greatest common divisor. This will give you the least common multiple of the two numbers. For example, 210 × 45 = 9450 {\displaystyle 210\times 45=9450} 210\times 45=9450. Dividing by the greatest common divisor, you get 9450 15 = 630 {\displaystyle {\frac {9450}{15}}=630} {\frac {9450}{15}}=630. So, 630 is the least common multiple of 210 and 45.