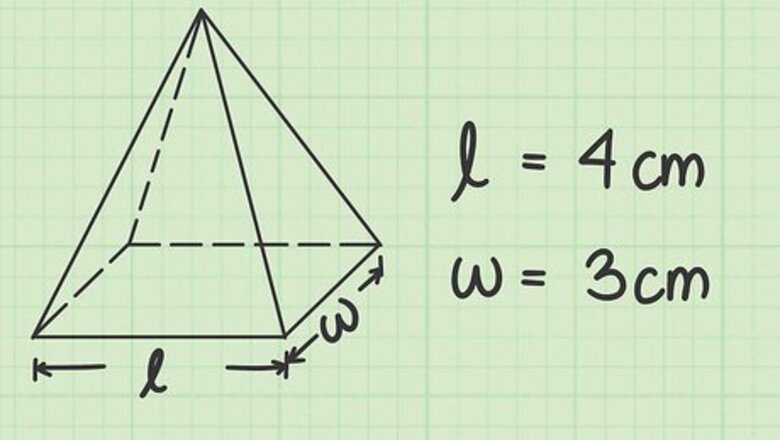
views
V
=
1
3
l
w
h
{\displaystyle V={\frac {1}{3}}lwh}
, where l and w are the length and width of the base, and h is the height. You can also use the equivalent formula
V
=
1
3
A
b
h
{\displaystyle V={\frac {1}{3}}A_{b}h}
, where
A
b
{\displaystyle A_{b}}
is the area of the base and h is the height. The method varies slightly depending on whether the pyramid has a triangular or a rectangular base. If you want to know how to calculate the volume of a pyramid, just follow these steps.
Pyramid with a Rectangular Base

Find the length and width of the base. In this example, the length of the base is 4 cm and the width is 3 cm. If you're working with a square base, the method is the same, except the length and width of the square base will be equal. Write down these measurements. Remember, V = 1 3 l w h = 1 3 A b h {\displaystyle V={\frac {1}{3}}lwh={\frac {1}{3}}A_{b}h} V={\frac {1}{3}}lwh={\frac {1}{3}}A_{{b}}h, so you need to know l {\displaystyle l} l and w {\displaystyle w} w first. l = 4 cm {\displaystyle l=4\,{\text{cm}}} l=4\,{\text{cm}} w = 3 cm {\displaystyle w=3\,{\text{cm}}} w=3\,{\text{cm}}
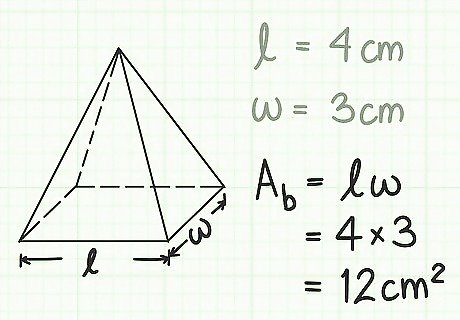
Multiply the length and width to find the area of the base. To get the area of the base, simply multiply 3 cm by 4 cm. Remember, V = 1 3 A b h {\displaystyle V={\frac {1}{3}}A_{b}h} V={\frac {1}{3}}A_{{b}}h, so you need to know A b {\displaystyle A_{b}} A_{{b}}. You can find this by plugging in l = 4 cm {\displaystyle l=4\,{\text{cm}}} l=4\,{\text{cm}} and w = 3 cm {\displaystyle w=3\,{\text{cm}}} w=3\,{\text{cm}} from the previous step. A b = l w {\displaystyle A_{b}=lw} A_{{b}}=lw A b = ( 4 cm ) ( 3 cm ) = 12 cm 2 {\displaystyle A_{b}=(4\,{\text{cm}})(3\,{\text{cm}})=12\,{\text{cm}}^{2}} A_{{b}}=(4\,{\text{cm}})(3\,{\text{cm}})=12\,{\text{cm}}^{2}

Multiply the area of the base by the height. The area of the base is 12 cm and the height is 4 cm, so you can multiply 12 cm by 4 cm. Remember, V = 1 3 A b h {\displaystyle V={\frac {1}{3}}A_{b}h} V={\frac {1}{3}}A_{{b}}h, so you need to know A b h {\displaystyle A_{b}h} A_{{b}}h. You can find this using A b {\displaystyle A_{b}} A_{{b}} from the previous step. A b = 12 cm 2 {\displaystyle A_{b}=12\,{\text{cm}}^{2}} A_{{b}}=12\,{\text{cm}}^{2} h = 4 cm {\displaystyle h=4\,{\text{cm}}} h=4\,{\text{cm}} A b h = ( 12 cm 2 ) ( 4 cm ) = 48 cm 3 {\displaystyle A_{b}h=(12\,{\text{cm}}^{2})(4\,{\text{cm}})=48\,{\text{cm}}^{3}} A_{{b}}h=(12\,{\text{cm}}^{2})(4\,{\text{cm}})=48\,{\text{cm}}^{3}

Multiply your result so far by 1 3 {\displaystyle {\frac {1}{3}}} {\frac {1}{3}}. Or, in other words, divide by 3. Remember to state your answer in cubic units whenever you're working with three-dimensional space. Remember, V = 1 3 l w h = 1 3 A b h {\displaystyle V={\frac {1}{3}}lwh={\frac {1}{3}}A_{b}h} V={\frac {1}{3}}lwh={\frac {1}{3}}A_{{b}}h. You can plug in A b h = 48 cm 3 {\displaystyle A_{b}h=48\,{\text{cm}}^{3}} A_{{b}}h=48\,{\text{cm}}^{3} from the previous step. V = 1 3 A b h {\displaystyle V={\frac {1}{3}}A_{b}h} V={\frac {1}{3}}A_{{b}}h V = ( 1 3 ) ( 48 cm 3 ) = 16 cm 3 {\displaystyle V=({\frac {1}{3}})(48\,{\text{cm}}^{3})=16\,{\text{cm}}^{3}} V=({\frac {1}{3}})(48\,{\text{cm}}^{3})=16\,{\text{cm}}^{3} EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher To find a pyramid's volume, use the formula (1/3) ∗ {\displaystyle *} * Base Area ∗ {\displaystyle *} * Height. Measure a pyramid's height from its tip to the base's center. Next, find the base area using the correct formula for the base shape, whether a triangle, square, or rectangle. Finally, input these values into the formula to calculate volume.
Pyramid with a Triangular Base
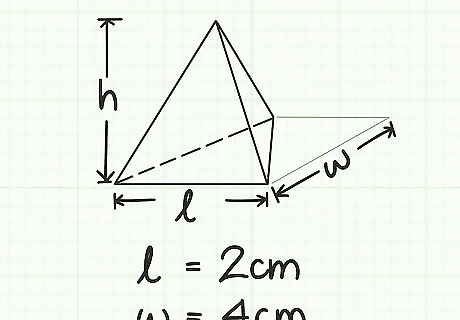
Find the length and width of the base. The length and width of the base must be perpendicular to each other for this method to work. They can also be considered the base and height of the triangle. In this example, the width of the base is 2 cm and the length of the triangle is 4 cm. If the length and width are not perpendicular and you don't know the height of the triangle, there are a few other methods you can try to calculate the area of a triangle. Remember, V = 1 3 l w h = 1 3 A b h {\displaystyle V={\frac {1}{3}}lwh={\frac {1}{3}}A_{b}h} V={\frac {1}{3}}lwh={\frac {1}{3}}A_{{b}}h, so you need to know l {\displaystyle l} l and w {\displaystyle w} w first. l = width of pyramid base = base of triangle, or b = 2 cm {\displaystyle l={\text{width of pyramid base}}={\text{base of triangle, or}}\,b=2\,{\text{cm}}} l={\text{width of pyramid base}}={\text{base of triangle, or}}\,b=2\,{\text{cm}} w = length of pyramid base = height of triangle, or h = 4 cm {\displaystyle w={\text{length of pyramid base}}={\text{height of triangle, or}}\,h=4\,{\text{cm}}} w={\text{length of pyramid base}}={\text{height of triangle, or}}\,h=4\,{\text{cm}}
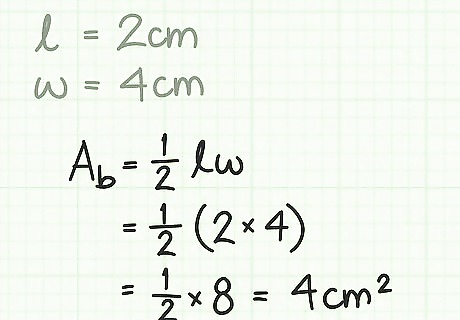
Calculate the area of the base. To calculate the area of the base, just plug the base and height of the triangle into the following formula: A b = 1 2 b h {\displaystyle A_{b}={\frac {1}{2}}bh} A_{{b}}={\frac {1}{2}}bh. Remember, V = 1 3 l w h = 1 3 A b h {\displaystyle V={\frac {1}{3}}lwh={\frac {1}{3}}A_{b}h} V={\frac {1}{3}}lwh={\frac {1}{3}}A_{{b}}h, so you need to know A b {\displaystyle A_{b}} A_{{b}}. You can find this using b {\displaystyle b} b and h {\displaystyle h} h from the previous step. A b = 1 2 b h {\displaystyle A_{b}={\frac {1}{2}}bh} A_{{b}}={\frac {1}{2}}bh A b = ( 1 2 ) ( 2 cm ) ( 4 cm ) {\displaystyle A_{b}=({\frac {1}{2}})(2\,{\text{cm}})(4\,{\text{cm}})} A_{{b}}=({\frac {1}{2}})(2\,{\text{cm}})(4\,{\text{cm}}) A b = ( 1 2 ) ( 8 cm 2 ) {\displaystyle A_{b}=({\frac {1}{2}})(8\,{\text{cm}}^{2})} A_{{b}}=({\frac {1}{2}})(8\,{\text{cm}}^{2}) A b = 4 cm 2 {\displaystyle A_{b}=4\,{\text{cm}}^{2}} A_{{b}}=4\,{\text{cm}}^{2}

Multiply the area of the base by the height of the pyramid. The area of the base is 4 cm and the height is 5 cm. Remember, V = 1 3 A b h {\displaystyle V={\frac {1}{3}}A_{b}h} V={\frac {1}{3}}A_{{b}}h, so you need to know A b h {\displaystyle A_{b}h} A_{{b}}h. You can find this using A b {\displaystyle A_{b}} A_{{b}} from the previous step. A b = area of triangular base = 4 cm 2 {\displaystyle A_{b}={\text{area of triangular base}}=4\,{\text{cm}}^{2}} A_{{b}}={\text{area of triangular base}}=4\,{\text{cm}}^{2} h = height of pyramid = 5 cm {\displaystyle h={\text{height of pyramid}}=5\,{\text{cm}}} h={\text{height of pyramid}}=5\,{\text{cm}} A b h = ( 4 cm 2 ) ( 5 cm ) = 20 cm 3 {\displaystyle A_{b}h=(4\,{\text{cm}}^{2})(5\,{\text{cm}})=20\,{\text{cm}}^{3}} A_{{b}}h=(4\,{\text{cm}}^{2})(5\,{\text{cm}})=20\,{\text{cm}}^{3}
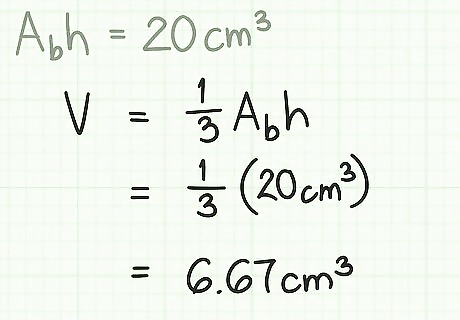
Multiply your result so far by 1 3 {\displaystyle {\frac {1}{3}}} {\frac {1}{3}}. Or, in other words, divide by 3. Your result will show that the volume of a pyramid with a height of 5 cm and a triangular base with a width of 2 cm and a length of 4 cm is 6.67 cm. Remember, V = 1 3 l w h = 1 3 A b h {\displaystyle V={\frac {1}{3}}lwh={\frac {1}{3}}A_{b}h} V={\frac {1}{3}}lwh={\frac {1}{3}}A_{{b}}h. You can plug in A b h = 20 cm 3 {\displaystyle A_{b}h=20\,{\text{cm}}^{3}} A_{{b}}h=20\,{\text{cm}}^{3} from the previous step. V = ( 1 3 ) A b h {\displaystyle V=({\frac {1}{3}})A_{b}h} V=({\frac {1}{3}})A_{{b}}h V = ( 1 3 ) ( 20 cm 3 ) = 6.67 cm 3 {\displaystyle V=({\frac {1}{3}})(20\,{\text{cm}}^{3})=6.67\,{\text{cm}}^{3}} V=({\frac {1}{3}})(20\,{\text{cm}}^{3})=6.67\,{\text{cm}}^{3}


















Comments
0 comment