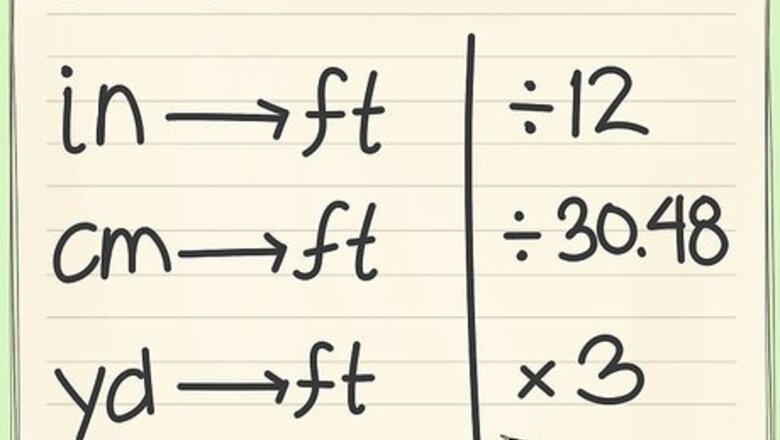
views
Finding Cubic Feet
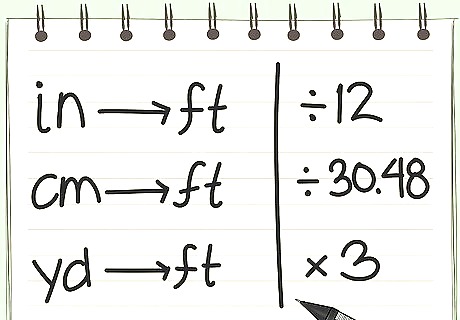
Make sure that all of your measurements are in feet. If you make one measurement in feet, you need to make them all in feet. You cannot measure the length in inches and the width in feet, otherwise your answer won't have any meaning. If you need to make the measurements yourself, make sure they are in the same scale. If you've been given different units, you can convert them as follows: If given inches... divide the measurement by 12 (ex. 24 i n 12 = 2 f t {\displaystyle {\frac {24in}{12}}=2ft} {\frac {24in}{12}}=2ft). If given centimeters... divide by 30.48 (ex. 150 c m 30.48 = 4.92126 f t {\displaystyle {\frac {150cm}{30.48}}=4.92126ft} {\frac {150cm}{30.48}}=4.92126ft). If given yards... multiply the measurement by 3 (ex. 3 y d s ∗ 3 = 9 f t {\displaystyle 3yds*3=9ft} 3yds*3=9ft).
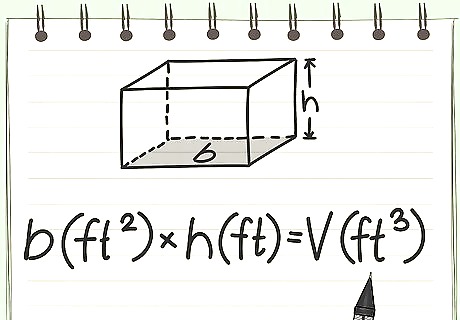
Convert to cubic feet easily for any regular, right prisms by multiplying by the height. A regular, right prism is simply a basic 3D shape like a rectangular box, a cylinder, etc: any shape with two even shapes on the ends and a smooth, regular connection between them. Finding an area's total cubic feet is a way to measure its volume, or how much room the three-dimensional space takes up. For regular prisms, such as rectangles, cylinders, and triangular prisms, all you have to know is the area of the base and the height. The area of the base is always in square footage, such as 2 f t 2 {\displaystyle 2ft^{2}} 2ft^{2}. If you've got a room you want cubic footage off, the base is the square footage of the floor. The height, or how tall the space is, is always measured from base to base, at the same point on each. So if you measure from the corner of the floor, you need to go to the same corner in the ceiling. A regular prism is one where the two bases are even and equal polygons, such as triangles, squares, circles, diamonds, etc.
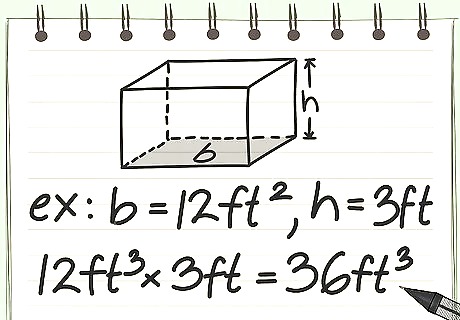
Multiply the base by the height to get the cubic footage of regular shapes. The easiest way to see this is to think of the volume of a rectangle, found using the basic formula L e n g t h ∗ W i d t h ∗ H e i g h t {\displaystyle Length*Width*Height} Length*Width*Height. Since square footage is found by multiplying length and width, all you have to do now is account for the height. This same principle applies no matter what the base is -- simply multiply square footage by height. Square Footage = 12 f t 2 {\displaystyle 12ft^{2}} 12ft^{2}, Height = 3 f t {\displaystyle 3ft} 3ft 12 f t 2 ∗ 3 f t = {\displaystyle 12ft^{2}*3ft=} 12ft^{2}*3ft= 36 cubic feet Square Footage = 4 f t 2 {\displaystyle 4ft^{2}} 4ft^{2}, Height = 6 f t {\displaystyle 6ft} 6ft 4 f t 2 ∗ 6 f t = {\displaystyle 4ft^{2}*6ft=} 4ft^{2}*6ft= 24 cubic feet Square Footage = 1.5 π f t 2 {\displaystyle 1.5\pi ft^{2}} 1.5\pi ft^{2}, Height = 2 f t {\displaystyle 2ft} 2ft 1.5 π f t 2 ∗ 2 f t = {\displaystyle 1.5\pi ft^{2}*2ft=} 1.5\pi ft^{2}*2ft= 9.42 cubic feet
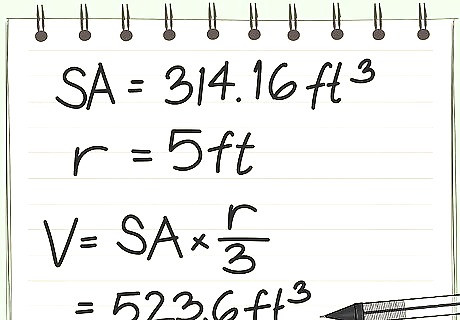
Convert the square footage of a sphere by multiplying the surface area by r 3 {\displaystyle {\frac {r}{3}}} {\frac {r}{3}}, where r is the sphere's radius. If you're given the surface area of a sphere and the radius, you can convert to cubic footage with ease. Simply multiply the surface area by the radius, then divide by three: Surface Area = 314.16 f t 2 {\displaystyle 314.16ft^{2}} 314.16ft^{2}, Radius= 5 f t {\displaystyle 5ft} 5ft 314.16 f t 2 ∗ 5 3 = {\displaystyle 314.16ft^{2}*{\frac {5}{3}}=} 314.16ft^{2}*{\frac {5}{3}}= 523.6 cubic feet Note, however, that the formula for the volume of a sphere is simply V = 4 3 π ∗ r 3 {\displaystyle V={\frac {4}{3}}\pi *r^{3}} V={\frac {4}{3}}\pi *r^{3} It is often easier to plug in "r" for this equation than to try and convert from square footage.

Always express your answer in cubic feet after solving. This is a simple way to keep track of measurements whether you're building a garden or finishing up your homework. To finish you answer, you must denote the type of measurements so that a builder, teacher, or friend knows whether "523.6" refers to inches, yards, feet, miles, etc. Remember: volume is always cubed. There are three acceptable ways to write the units for cubic feet. 523.6 f t 3 {\displaystyle 523.6ft^{3}} 523.6ft^{3} 523.6 {\displaystyle 523.6} 523.6 cubic feet. 523.6 {\displaystyle 523.6} 523.6 feet cubed
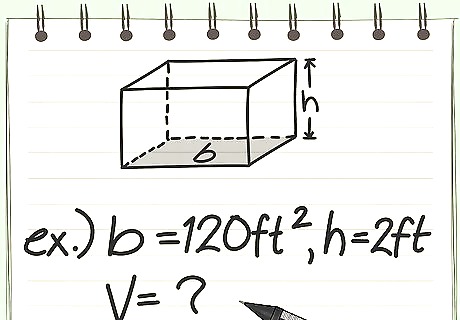
Practice with an example. The following question should not be difficult, as long as you remember how the correct equation. The answer can be found by clicking and highlighting after the second bullet. You have a carrot and potato garden with a square footage of 120 f t 2 {\displaystyle 120ft^{2}} 120ft^{2}. The bed is two feet deep. What is the volume of the garden in cubic feet? The cubic feet measurement is 240 f t 3 {\displaystyle 240ft^{3}} 240ft^{3} ( 120 f t 2 x 2 f t = 240 f t 3 ) {\displaystyle (120ft^{2}x2ft=240ft^{3})} (120ft^{2}x2ft=240ft^{3})
Understanding and Using Your Measurements

Know how to spot questions asking for cubic footage. Not all questions are going to tell you outright that they want you to find cubic footage. What you need to remember is that cubic footage is just a measurement of volume -- so any volume question you're asked with feet in the measurements ( f t 3 {\displaystyle ft^{3}} ft^{3}), is likely asking for cubic feet. Some example problems might ask: If the square footage is 10 f t 2 {\displaystyle 10ft^{2}} 10ft^{2}, and the height is 5 f t {\displaystyle 5ft} 5ft, what is the volume? What is the volume, in feet, of the garden? How many cubic feet of water could fit in a square box with a base of 23 f t 2 {\displaystyle 23ft^{2}} 23ft^{2} and a height of 2 f t {\displaystyle 2ft} 2ft? (Note: "base" means the flat bottom, or square footage.
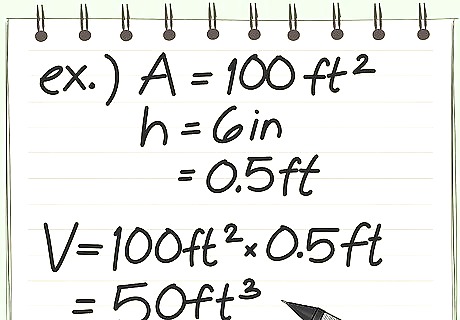
Purchase mulch, soil, and other commodities sold by cubic footage only after you know the thickness you need for your project. This is best seen in an example. Say you have a 100 square foot backyard area to plant a garden and need to know how much topsoil to buy. Before buying anything, you need to know how deep your soil will go. This is your "height" measurement, telling you how high the soil must go. For example, say you need, at minimum 6-inch holes for each plant: Make sure all units are in feet: 6 i n 12 = .5 f t {\displaystyle {\frac {6in}{12}}=.5ft} {\frac {6in}{12}}=.5ft Multiply square footage by height: 100 ∗ .5 = 50 {\displaystyle 100*.5=50} 100*.5=50 Express answer in cubic feet You must purchase at least 50 f t 3 {\displaystyle 50ft^{3}} 50ft^{3} of soil to fill your garden.
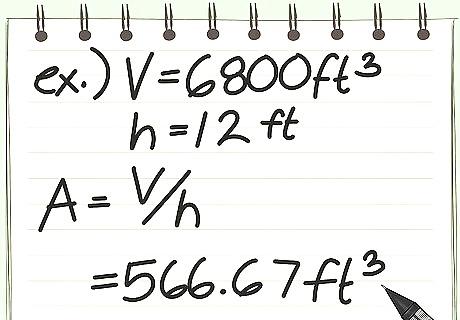
Convert cubic feet back into square footage by dividing the height from the cubic footage. Since it is such a simple conversion to get to square footage, it is simple to undo. For example, you might have a heater capable of filling a 6800 f t 3 {\displaystyle 6800ft^{3}} 6800ft^{3}, but you want to know how much floor-space that covers in your room. To find out, simply divide 6800 by the height of the room, found by simply measuring floor to ceiling: Example height of the room = 12 f t {\displaystyle 12ft} 12ft 6800 f t 3 12 f r = 566.67 f t 2 {\displaystyle {\frac {6800ft^{3}}{12fr}}=566.67ft^{2}} {\frac {6800ft^{3}}{12fr}}=566.67ft^{2} The heater will heat a room with a square footage is 566.67 f t 2 {\displaystyle 566.67ft^{2}} 566.67ft^{2} and a height of 12ft. This strategy is purely for rectangular or cylindrical volumes. It is much more complex for pyramids and spheres.
Remember that this conversion only works for regular prisms and spheres. If your shape curves, bends, twists, or is otherwise irregular, you cannot simply convert from square footage to cubic footage. If the object changes size or thickness as it gains height than the measurement of the base -- your square footage -- will no longer be accurate. These types of problems usually require the integral calculus to solve. Imagine buying a heater for a room with a pointed ceiling. Now imagine how much more of the room you'd have to heat if the room was perfectly square, instead of pointed at the top. While the square footage of the floor is important, it isn't the only thing determining the cubic footage.
















Comments
0 comment