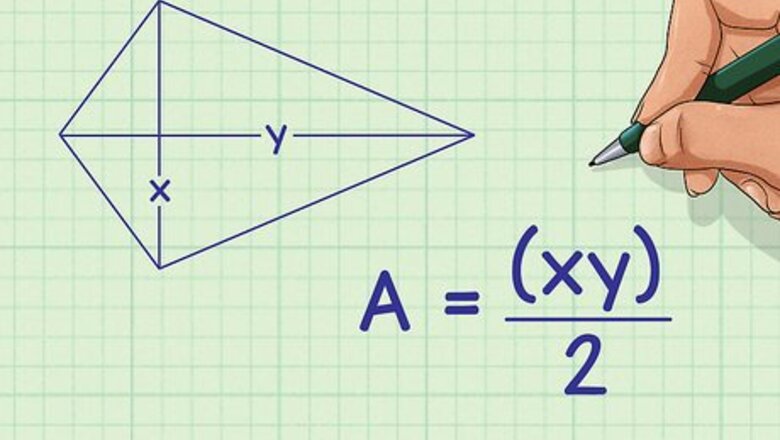
views
X
Research source
Kites can take the traditional look of a flying kite, but a kite can also be a rhombus or a square.[2]
X
Research source
No matter what a kite looks like, the methods for finding the area will be the same. If you know the length of the diagonals, you can find the area through simple algebra. You can also use trigonometry to find the area, if you know the side and angle measurements of the figure.
Using the Diagonals to Find the Area
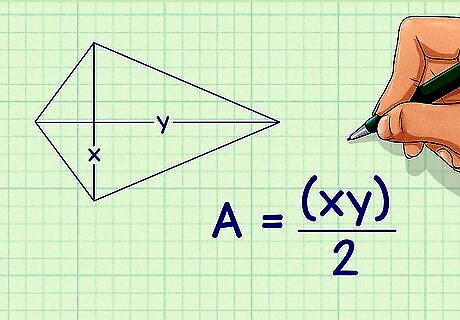
Set up the formula for the area of a kite, given two diagonals. The formula is A = x y 2 {\displaystyle A={\frac {xy}{2}}} A={\frac {xy}{2}}, where A {\displaystyle A} A equals the area of the kite, and x {\displaystyle x} x and y {\displaystyle y} y equal the lengths of the diagonals of the kite.
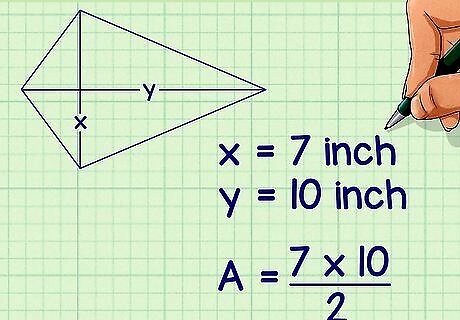
Plug the lengths of the diagonals into the formula. A diagonal is a straight line that runs from one vertex to the vertex on the opposite side. You should either be given the length of the diagonals, or be able to measure them. If you don’t know the length of the diagonals, you cannot use this method. For example, if a kite has two diagonals measuring 7 inches and 10 inches, your formula will look like this: A = 7 × 10 2 {\displaystyle A={\frac {7\times 10}{2}}} A={\frac {7\times 10}{2}}.
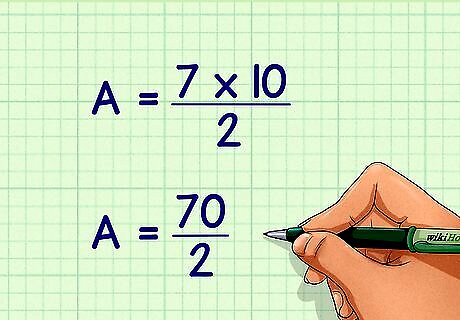
Multiply the lengths of the diagonals. The product becomes the new numerator in the area equation. For example: A = 7 × 10 2 {\displaystyle A={\frac {7\times 10}{2}}} A={\frac {7\times 10}{2}} A = 70 2 {\displaystyle A={\frac {70}{2}}} A={\frac {70}{2}}
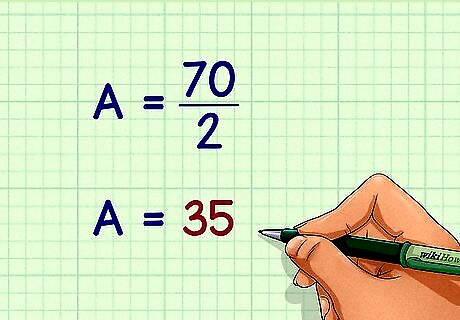
Divide the product of the diagonals by 2. This will give you the area of the kite, in square units. For example: A = 70 2 {\displaystyle A={\frac {70}{2}}} A={\frac {70}{2}} A = 35 {\displaystyle A=35} A=35So, the area of a kite with diagonals measuring 10 inches and 7 inches is 35 square inches.
Using an Angle and Two Sides to Find the Area
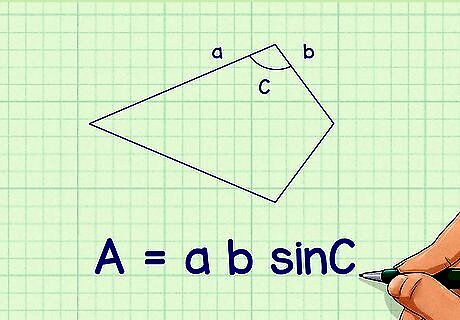
Set up the formula for the area of a kite. This formula works if you are given two non-congruent side lengths and the size of the angle between those two sides. The formula is A = a b sin C {\displaystyle A=ab\sin C} A=ab\sin C, where A {\displaystyle A} A equals the area of the kite, a {\displaystyle a} a and b {\displaystyle b} b equal the non-congruent side lengths of the kite, and C {\displaystyle C} C equals the size of the angle between sides a {\displaystyle a} a and b {\displaystyle b} b. Make sure you are using two non-congruent side lengths. A kite has two pairs of congruent sides. You need to use one side from each pair. Make sure the angle measurement you use is the angle between these two sides. If you do not have all of this information, you cannot use this method.
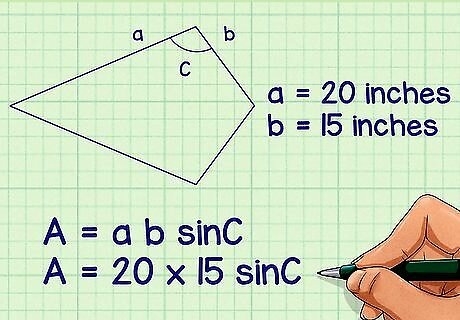
Plug the length of the sides into the formula. This information should be given, or you should be able to measure them. Remember that you are using non-congruent sides, so each side should have a different length. For example, if your kite has a side length of 20 inches and a side length of 15 inches, your formula will look like this: A = 20 × 15 sin C {\displaystyle A=20\times 15\sin C} A=20\times 15\sin C.
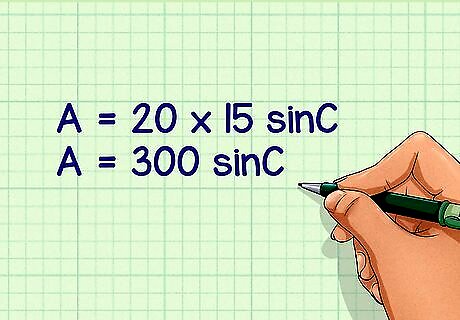
Multiply the side lengths. Plug this product into the formula. For example: A = 20 × 15 sin C {\displaystyle A=20\times 15\sin C} A=20\times 15\sin C A = 300 sin C {\displaystyle A=300\sin C} A=300\sin C
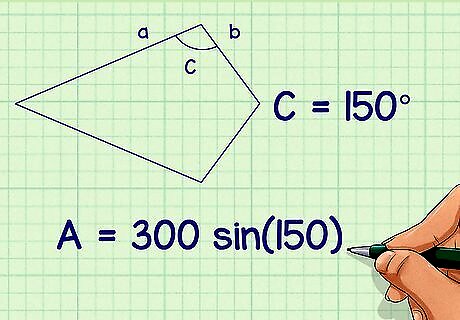
Plug the angle measurement into the formula. Make sure you are using the angle between the two non-congruent sides. For example, if the angle measurement is 150 ∘ {\displaystyle 150^{\circ }} 150^{\circ }, your formula will look like this: A = 300 sin ( 150 ) {\displaystyle A=300\sin(150)} A=300\sin(150).
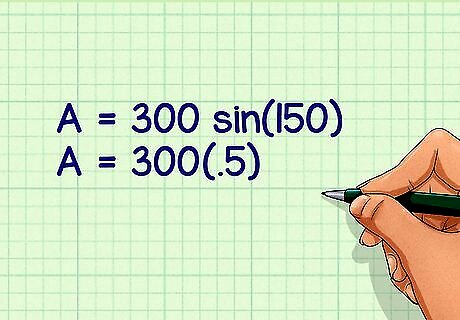
Find the sine of the angle. To do this, you can use a calculator, or use a trigonometry chart. For example, the sine of a 150 degree angle is .5, so your formula will look like this: A = 300 ( .5 ) {\displaystyle A=300(.5)} A=300(.5).

Multiply the product of the sides by the sine of the angle. This result will be the area of the kite, in square units. For example: A = 300 ( .5 ) {\displaystyle A=300(.5)} A=300(.5) A = 150 {\displaystyle A=150} A=150So, the area of a kite, with two sides measuring 20 inches and 15 inches, and the angle between them measuring 150 degrees, is 150 square inches.
Using the Area to Find a Missing Diagonal

Set up the formula for the area of a kite, given two diagonals. The formula is A = x y 2 {\displaystyle A={\frac {xy}{2}}} A={\frac {xy}{2}}, where A {\displaystyle A} A equals the area of the kite, and x {\displaystyle x} x and y {\displaystyle y} y equal the lengths of the diagonals of the kite.
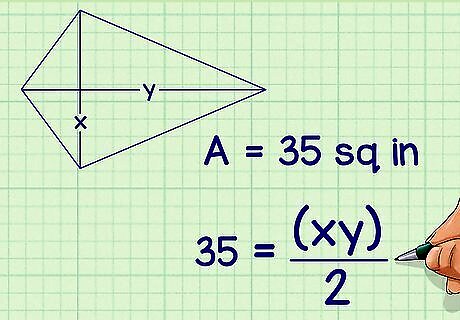
Plug the area of the kite into the formula. This information should be given to you. Make sure you are substituting for A {\displaystyle A} A. For example, if your kite has an area of 35 square inches, your formula will look like this: 35 = x y 2 {\displaystyle 35={\frac {xy}{2}}} 35={\frac {xy}{2}}.
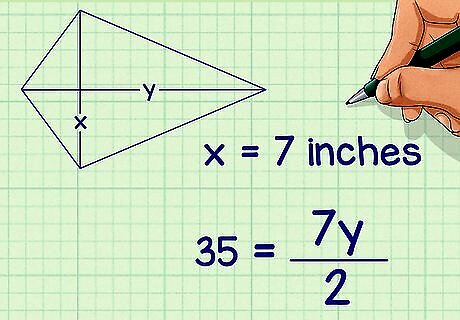
Plug the length of the known diagonal into the formula. Substitute for x {\displaystyle x} x. For example, if you know one of the diagonals is 7 inches long, your formula will look like this: 35 = 7 y 2 {\displaystyle 35={\frac {7y}{2}}} 35={\frac {7y}{2}}.
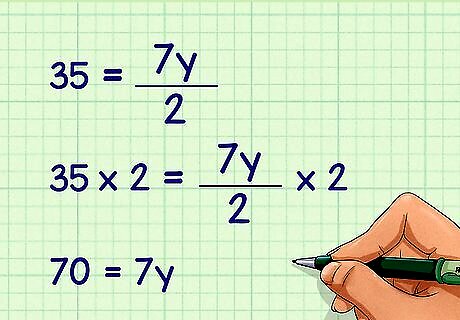
Multiply each side of the equation by 2. This will remove the fraction in the formula. For example: 35 = 7 y 2 {\displaystyle 35={\frac {7y}{2}}} 35={\frac {7y}{2}} 35 × 2 = 7 y 2 × 2 {\displaystyle 35\times 2={\frac {7y}{2}}\times 2} 35\times 2={\frac {7y}{2}}\times 2 70 = 7 y {\displaystyle 70=7y} 70=7y
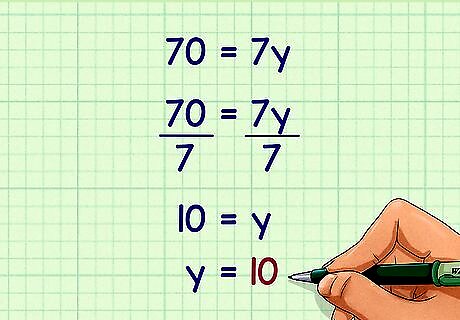
Divide each side of the equation by the length of the diagonal. This will give you the length of the missing diagonal. For example: 70 = 7 y {\displaystyle 70=7y} 70=7y 70 7 = 7 y 7 {\displaystyle {\frac {70}{7}}={\frac {7y}{7}}} {\frac {70}{7}}={\frac {7y}{7}} 10 = y {\displaystyle 10=y} 10=ySo, the length of the missing diagonal of a kite, given an area of 35 square inches and one diagonal of 7 inches, is 10 inches.
















Comments
0 comment