How to Multiply Factorials

Understanding Factorials

Identify a factorial. A factorial, denoted by a whole number with an exclamation point, is the product of a series of sequential whole numbers. For example, 6 ! {\displaystyle 6!} 6! is a factorial. Keep in mind that the factorial of 0 (0!) is 1 by convention. There also isn't any definition for the factorial of negative numbers—it's only possible to calculate the factorial of 0 and other positive numbers.

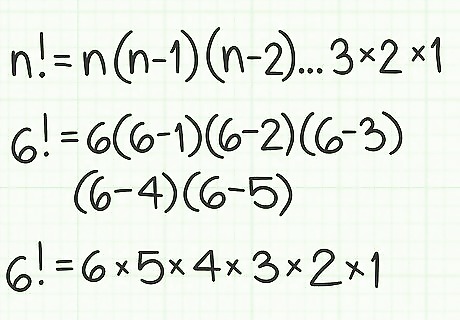
Evaluate a factorial using a formula. The formula is n ! = n ( n − 1 ) ( n − 2 ) ⋅ ⋅ ⋅ 3 ⋅ 2 ⋅ 1 {\displaystyle n!=n(n-1)(n-2)\cdot \cdot \cdot 3\cdot 2\cdot 1} n!=n(n-1)(n-2)\cdot \cdot \cdot 3\cdot 2\cdot 1. This means that you extend the sequence of numbers until you get to 1. For example, 6 ! = 6 ( 6 − 1 ) ( 6 − 2 ) ( 6 − 3 ) ( 6 − 4 ) ( 6 − 5 ) = 6 ( 5 ) ( 4 ) ( 3 ) ( 2 ) ( 1 ) {\displaystyle 6!=6(6-1)(6-2)(6-3)(6-4)(6-5)=6(5)(4)(3)(2)(1)} 6!=6(6-1)(6-2)(6-3)(6-4)(6-5)=6(5)(4)(3)(2)(1)

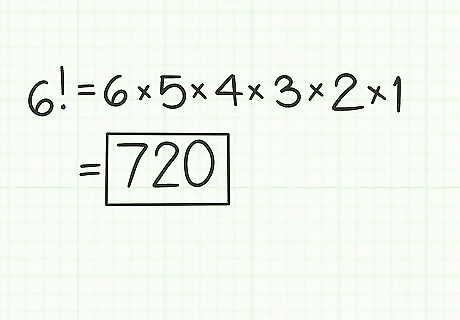
Calculate a factorial. To calculate a factorial, begin with the denoted number, and multiply it by each sequential whole number, down to 1. A quick way to calculate a factorial is to use the x ! {\displaystyle x!} x! key on a scientific calculator. First hit the number, then hit the x ! {\displaystyle x!} x! key to see the product. For example, 6 ! = 6 × 5 × 4 × 3 × 2 × 1 = 720 {\displaystyle 6!=6\times 5\times 4\times 3\times 2\times 1=720} 6!=6\times 5\times 4\times 3\times 2\times 1=720.

Calculating the Factorials Separately

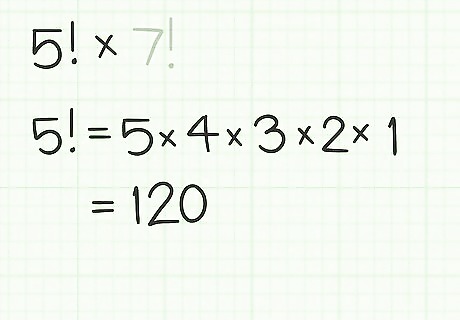
Calculate the first factorial. Use a calculator for larger numbers. If calculating by hand, make sure you multiply each sequential number, down to 1. Rewrite the equation with this product in parentheses as the first factor. For example, if you are calculating 5 ! × 7 ! {\displaystyle 5!\times 7!} 5!\times 7!, first calculate 5 ! {\displaystyle 5!} 5!: 5 ! × 7 ! {\displaystyle 5!\times 7!} 5!\times 7! = ( 5 × 4 × 3 × 2 × 1 ) × ( 7 ! ) {\displaystyle =(5\times 4\times 3\times 2\times 1)\times (7!)} =(5\times 4\times 3\times 2\times 1)\times (7!) = ( 120 ) × ( 7 ! ) {\displaystyle =(120)\times (7!)} =(120)\times (7!)

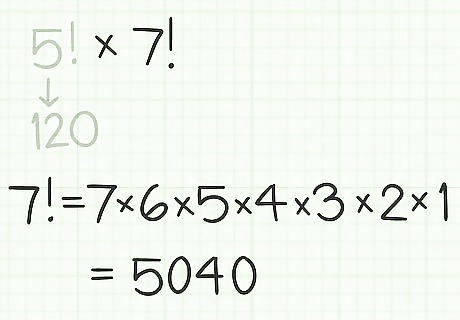
Calculate the second factorial. You can do this by calculator or by hand, beginning on the complexity of the factorial. Rewrite the equation with this product as the second factor. For example: ( 120 ) × ( 7 ! ) {\displaystyle (120)\times (7!)} (120)\times (7!) = ( 120 ) × ( 7 × 6 × 5 × 4 × 3 × 2 × 1 ) {\displaystyle =(120)\times (7\times 6\times 5\times 4\times 3\times 2\times 1)} =(120)\times (7\times 6\times 5\times 4\times 3\times 2\times 1) = ( 120 ) × ( 5040 ) {\displaystyle =(120)\times (5040)} =(120)\times (5040)

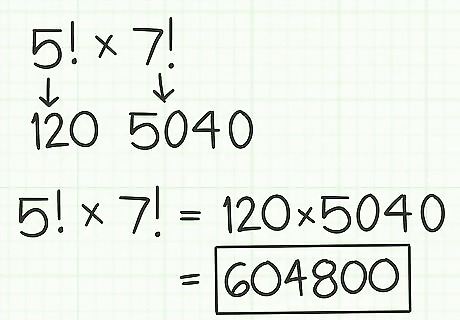
Multiply the two factorials’ products. This will give you the product of the two factorials. Since factorials tend to be large numbers, using a calculator will make this calculation easier. For example, ( 120 ) × ( 5040 ) = 604 , 800 {\displaystyle (120)\times (5040)=604,800} (120)\times (5040)=604,800. So, 5 ! × 7 ! = 604 , 800 {\displaystyle 5!\times 7!=604,800} 5!\times 7!=604,800.

Finding Common Factors

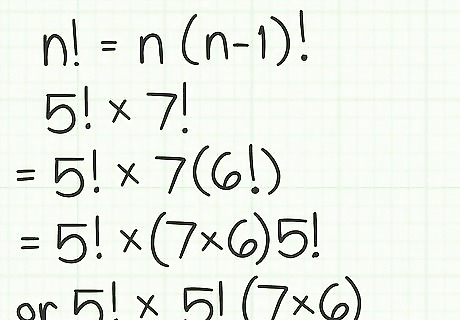
Use a formula to factor out the largest common factorial. The formula is n ! = n × ( n − 1 ) ! {\displaystyle n!=n\times (n-1)!} n!=n\times (n-1)!. This means that a smaller factorial is a factor of a larger factorial. For example, 4 ! = 4 × ( 4 − 1 ) ! = 4 × 3 ! {\displaystyle 4!=4\times (4-1)!=4\times 3!} 4!=4\times (4-1)!=4\times 3!. When you are multiplying two factorials, the largest common factorial is the smaller of the two factorials. For example, if you are calculating 5 ! × 7 ! {\displaystyle 5!\times 7!} 5!\times 7!, you can factor out 5 ! {\displaystyle 5!} 5! from 7 ! {\displaystyle 7!} 7!: 5 ! × 5 ! ( 7 × 6 ) {\displaystyle 5!\times 5!(7\times 6)} 5!\times 5!(7\times 6)

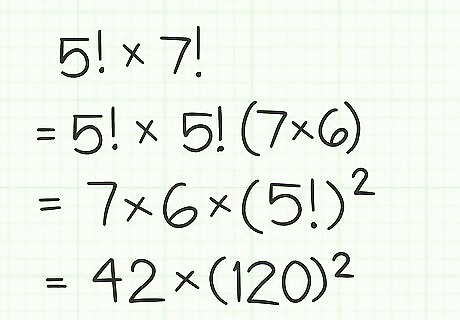
Rewrite the equation, showing the common factorial as a squared value. Then, calculate the factorial and square its product. For example, 5 ! × 5 ! ( 7 × 6 ) {\displaystyle 5!\times 5!(7\times 6)} 5!\times 5!(7\times 6) = 7 × 6 × ( 5 ! ) 2 {\displaystyle =7\times 6\times (5!)^{2}} =7\times 6\times (5!)^{{2}} = 42 × ( 120 ) 2 {\displaystyle =42\times (120)^{2}} =42\times (120)^{{2}}

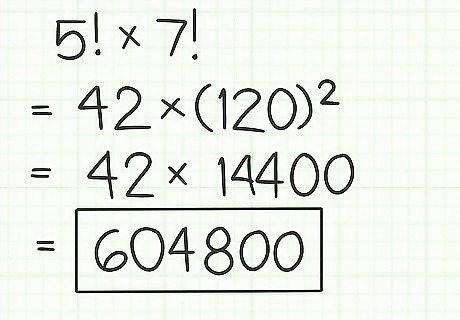
Multiply the remaining factors. The result will be the product of the two original factorials. For example: 42 × ( 120 ) 2 {\displaystyle 42\times (120)^{2}} 42\times (120)^{{2}} = 42 × 14 , 400 {\displaystyle =42\times 14,400} =42\times 14,400 = 604 , 800 {\displaystyle =604,800} =604,800