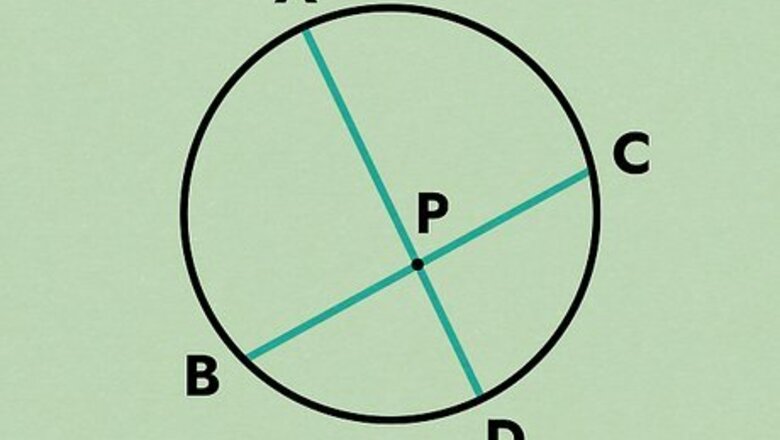
How to Prove the Intersecting Chords Theorem of Euclid

Swecopy

Editor

posted on 11 years ago — updated on 1 second ago

45
views

In geometry, the Intersecting Chords Theorem of Euclid is a statement that describes the relationship between 4 line segments created by 2 intersecting chords in a circle. Euclid’s theorem states that the products of the lengths of the line segments on each chord are equal. You can prove this mathematically with a few simple steps and a diagram. Keep reading to learn how to prove the Intersecting Chords Theorem of Euclid.

Steps

Draw a diagram of the Intersecting Chords Theorem.

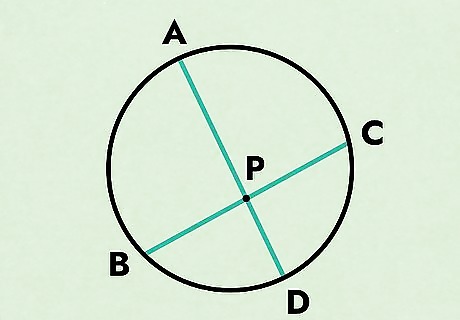
Drawing a diagram will help you visualize what you’re proving. The Intersecting Chords Theorem of Euclid states that given a point (P) in a circle and 2 chords (or lines) that pass through that circle (AD and BC), then ( A P ) ( D P ) = ( B P ) ( C P ) {\displaystyle (AP)(DP)=(BP)(CP)} {\displaystyle (AP)(DP)=(BP)(CP)}. Draw a circle and then mark A, B, C, D, and P. P is typically in the middle of the circle, but slightly off-center. Both the A,B line and the C,D line will intersect that point.

Join A, B and C, D to create 2 triangles.

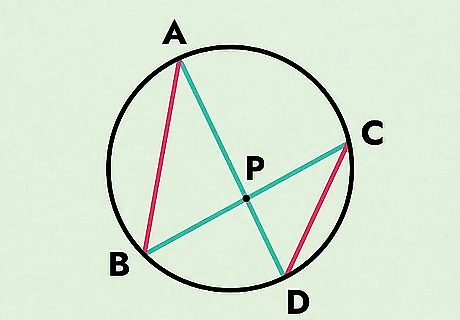
Prove this theorem by connecting the points to create triangles. Connect the points ABP to create 1 triangle, then connect CDP to create the second one.

Measure the angles of each triangle.

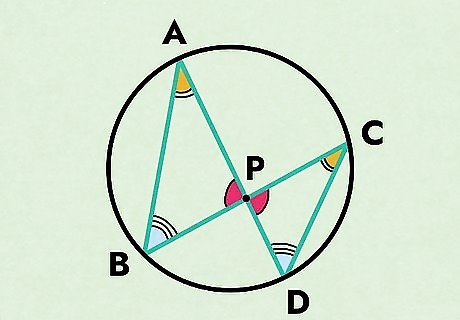
APB = CPD because they are opposite angles. Check out your triangles and identify all of the angles. By doing this, you can tell that A P B = C P D {\displaystyle APB=CPD} {\displaystyle APB=CPD} because they’re opposite angles. You can either measure all the angles by hand, or you can use the vertical angles theorem (when two straight lines intersect, they form two sets of linear pairs with congruent angles) to prove that ABP and CDP are the same. Then, you can use the inscribed angle theorem (an angle inscribed in a circle is half of the central angle that is on the same arc on the circle) to prove that angle A and angle C are equal. Finally, use the inscribed angle theorem again to prove that angle B and angle D are equal.

Compare the angles of the triangles.

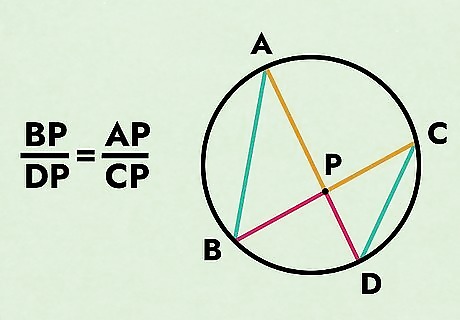
Use B P / D P = A P / C P {\displaystyle BP/DP=AP/CP} {\displaystyle BP/DP=AP/CP} to prove the triangles are similar. You’ll notice that both of your triangles have the same angles. Compile your similar points into fractions so that you can multiply them.

Cross multiply the ratios.

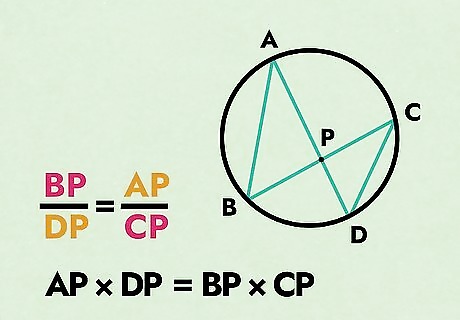
Multiplying the ratios proves the Chords Theorem of Euclid. Simply multiply ( B P ) ( C P ) = ( A P ) ( D P ) {\displaystyle (BP)(CP)=(AP)(DP)} {\displaystyle (BP)(CP)=(AP)(DP)}. The answer is ( A P ) ( D P ) = ( B P ) ( C P ) {\displaystyle (AP)(DP)=(BP)(CP)} {\displaystyle (AP)(DP)=(BP)(CP)}, which proves the Intersecting Chords Theorem of Euclid.