
views

Press the STAT button on your calculator. It's in the third column of keys.
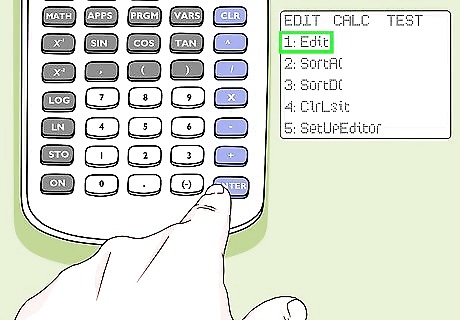
Select the Edit menu and press ↵ Enter. It's the first option on the menu. You will see columns (lists) labeled L1 through L6. Note: The TI-84 allows you to enter up to six different lists of data sets.

Clear existing data from the lists. If there's already data in any of the columns, use these steps to remove it before you continue: Use the arrow keys to navigate to L1 (the first column). Press ⎚ Clear. Press ↵ Enter. Repeat for other lists with data.
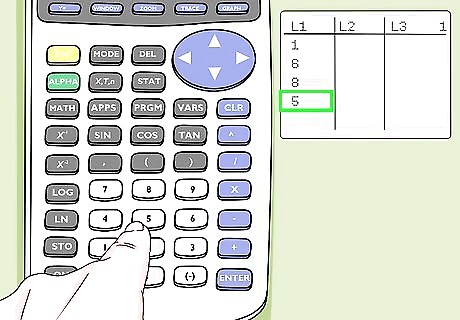
Enter your data set into the L1 column. Press the ↵ Enter key after each value.

Press the STAT button to return to the menu.

Press the right-arrow to switch to the CALC tab. It's the second menu tab at the top of the screen.

Select 1-Var Stats and press ↵ Enter.

Press the 2ND button and then 1 to select L1. You'll only need to do this if you have a T1-84 Plus model and don't already see "L1" next to "List." Tip: If you created multiple lists and want to select a different one, press the number that corresponds with that column. For example, if you want standard deviation for the values you entered in L4, press the 2ND and then 4. Some non-plus models may skip this screen and display your results automatically.

Select Calculate and press ↵ Enter. The TI-84 will now display standard deviation calculations for the set of values.

Find the standard deviation value next to Sx or σx. These should be the 4th and 5th results in the list. You may have to scroll down to view both values. Sx shows the standard deviation for a sample, while σx shows the standard deviation for a population. The value you'll use depends on whether you used data from a sample or a full population. A lower standard deviation value means that the values in your list don't vary much from the mean, while a higher value means your data is more spread out. x̄ represents the mean, or average, of the values. Σx represents the sum of all values.


















Comments
0 comment