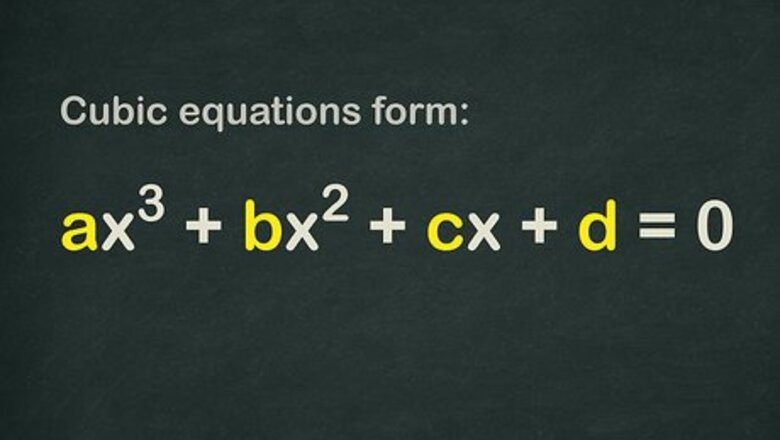
views
a
x
3
+
b
x
2
+
c
x
+
d
=
0
{\displaystyle ax^{3}+bx^{2}+cx+d=0}
.[1]
X
Research source
While cubics look intimidating and unlike quadratic equation is quite difficult to solve, using the right approach (and a good amount of foundational knowledge) can tame even the trickiest cubics. You can try, among other options, using the quadratic formula, finding integer solutions, or identifying discriminants.
Solving Cubic Equations without a Constant
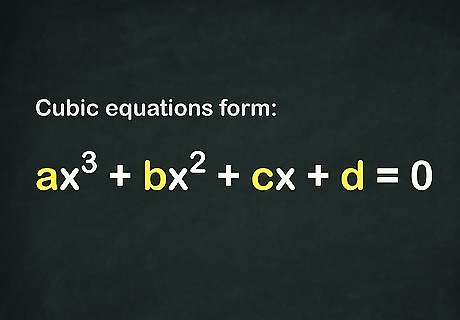
Check whether your cubic contains a constant (a d {\displaystyle d} d value). Cubic equations take the form a x 3 + b x 2 + c x + d = 0 {\displaystyle ax^{3}+bx^{2}+cx+d=0} ax^{3}+bx^{2}+cx+d=0. However, the only essential requirement is x 3 {\displaystyle x^{3}} x^{3}, which means the other elements need not be present to have a cubic equation. If your equation does contain a constant (a d {\displaystyle d} d value), you'll need to use another solving method. If a = 0 {\displaystyle a=0} a=0, you do not have a cubic equation.
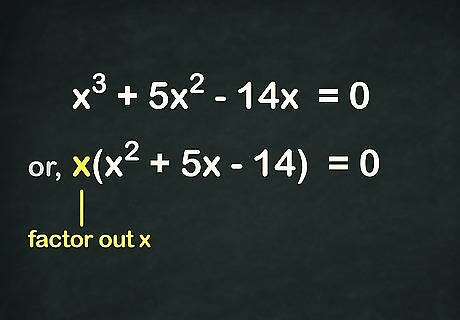
Factor an x {\displaystyle x} x out of the equation. Since your equation doesn't have a constant, every term in the equation has an x {\displaystyle x} x variable in it. This means that one x {\displaystyle x} x can be factored out of the equation to simplify it. Do this and re-write your equation in the form x ( a x 2 + b x + c ) {\displaystyle x(ax^{2}+bx+c)} x(ax^{2}+bx+c). For example, let's say that your starting cubic equation is 3 x 3 + 5 x 2 − 14 x = 0 {\displaystyle 3x^{3}+5x^{2}-14x=0} {\displaystyle 3x^{3}+5x^{2}-14x=0} Factoring a single x {\displaystyle x} x out of this equation, you get x ( 3 x 2 + 5 x − 14 ) = 0 {\displaystyle x(3x^{2}+5x-14)=0} {\displaystyle x(3x^{2}+5x-14)=0}
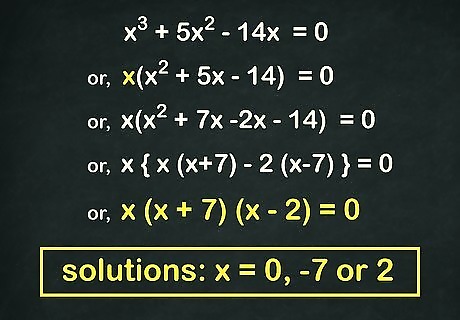
Factor the resulting quadratic equation, if possible. In many cases, you will be able to factor the quadratic equation ( a x 2 + b x + c {\displaystyle ax^{2}+bx+c} ax^{2}+bx+c) that results when you factor the x {\displaystyle x} x out. For example, if you are given x 3 + 5 x 2 − 14 x = 0 {\displaystyle x^{3}+5x^{2}-14x=0} x^{3}+5x^{2}-14x=0, then you can do the following: Factor out the x {\displaystyle x} x: x ( x 2 + 5 x − 14 ) = 0 {\displaystyle x(x^{2}+5x-14)=0} x(x^{2}+5x-14)=0 Factor the quadratic in parentheses: x ( x + 7 ) ( x − 2 ) = 0 {\displaystyle x(x+7)(x-2)=0} x(x+7)(x-2)=0 Set each of these factors equal to 0 {\displaystyle 0} {\displaystyle 0}. Your solutions are x = 0 , x = − 7 , x = 2 {\displaystyle x=0,x=-7,x=2} x=0,x=-7,x=2. You can also factor it by grouping.

Solve the portion in parentheses with the quadratic formula if you can’t factor it manually. You can find the values for which this quadratic equation equals 0 {\displaystyle 0} {\displaystyle 0} by plugging a {\displaystyle a} a, b {\displaystyle b} b, and c {\displaystyle c} c into the quadratic formula ( − b ± b 2 − 4 a c 2 a {\displaystyle {\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}} {\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}). Do this to find two of the answers to your cubic equation. In the example, plug your a {\displaystyle a} a, b {\displaystyle b} b, and c {\displaystyle c} c values ( 3 {\displaystyle 3} 3, − 2 {\displaystyle -2} -2, and 14 {\displaystyle 14} 14, respectively) into the quadratic equation as follows: − b ± b 2 − 4 a c 2 a {\displaystyle {\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}} {\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}} − ( − 2 ) ± ( ( − 2 ) 2 − 4 ( 3 ) ( 14 ) 2 ( 3 ) {\displaystyle {\frac {-(-2)\pm {\sqrt {((-2)^{2}-4(3)(14)}}}{2(3)}}} {\frac {-(-2)\pm {\sqrt {((-2)^{2}-4(3)(14)}}}{2(3)}} 2 ± 4 − ( 12 ) ( 14 ) 6 {\displaystyle {\frac {2\pm {\sqrt {4-(12)(14)}}}{6}}} {\frac {2\pm {\sqrt {4-(12)(14)}}}{6}} 2 ± ( 4 − 168 6 {\displaystyle {\frac {2\pm {\sqrt {(4-168}}}{6}}} {\frac {2\pm {\sqrt {(4-168}}}{6}} 2 ± − 164 6 {\displaystyle {\frac {2\pm {\sqrt {-164}}}{6}}} {\frac {2\pm {\sqrt {-164}}}{6}} Answer 1: 2 + − 164 6 {\displaystyle {\frac {2+{\sqrt {-164}}}{6}}} {\frac {2+{\sqrt {-164}}}{6}} 2 + 12.8 i 6 {\displaystyle {\frac {2+12.8i}{6}}} {\frac {2+12.8i}{6}} Answer 2: 2 − 12.8 i 6 {\displaystyle {\frac {2-12.8i}{6}}} {\frac {2-12.8i}{6}}
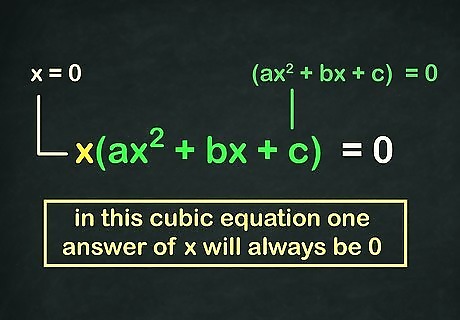
Use zero and the quadratic answers as your cubic's answers. While quadratic equations have two solutions, cubics have three. You already have two of these — they're the answers you found for the "quadratic" portion of the problem in parentheses. In cases where your equation is eligible for this "factoring" method of solving, your third answer will always be 0 {\displaystyle 0} {\displaystyle 0}. Factoring your equation into the form x ( a x 2 + b x + c ) = 0 {\displaystyle x(ax^{2}+bx+c)=0} x(ax^{2}+bx+c)=0 splits it into two factors: one factor is the x {\displaystyle x} x variable on the left, and the other is the quadratic portion in parentheses. If either of these factors equals 0 {\displaystyle 0} {\displaystyle 0}, the entire equation will equal 0 {\displaystyle 0} {\displaystyle 0}. Thus, the two answers to the quadratic portion in parentheses, which will make that factors equal 0 {\displaystyle 0} {\displaystyle 0}, are answers to the cubic, as is 0 {\displaystyle 0} {\displaystyle 0} itself, which will make the left factor equal 0 {\displaystyle 0} {\displaystyle 0}.
Finding Integer Solutions with Factor Lists
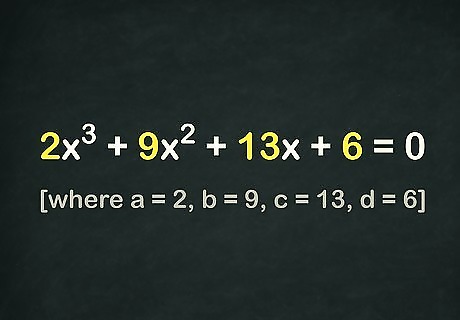
Ensure your cubic has a constant (a nonzero d {\displaystyle d} d value). If your equation in the form a x 3 + b x 2 + c x + d = 0 {\displaystyle ax^{3}+bx^{2}+cx+d=0} ax^{3}+bx^{2}+cx+d=0 has a nonzero value for d {\displaystyle d} d, factoring with the quadratic equation won't work. But don’t worry—you have other options, like the one described here! Take, for example, 2 x 3 + 9 x 2 + 13 x = − 6 {\displaystyle 2x^{3}+9x^{2}+13x=-6} 2x^{3}+9x^{2}+13x=-6. In this case, getting a 0 {\displaystyle 0} {\displaystyle 0} on the right side of the equals sign requires you to add 6 {\displaystyle 6} 6 to both sides. In the new equation, 2 x 3 + 9 x 2 + 13 x + 6 = 0 {\displaystyle 2x^{3}+9x^{2}+13x+6=0} 2x^{3}+9x^{2}+13x+6=0. Since d = 6 {\displaystyle d=6} d=6, you can't use the quadratic equation method.
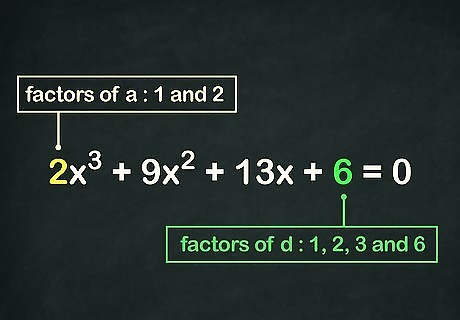
Find the factors of a {\displaystyle a} a and d {\displaystyle d} d. Start solving the cubic equation by finding the factors of the coefficient of the x 3 {\displaystyle x^{3}} x^{3} term (that is, a {\displaystyle a} a) and the constant at the end of the equation (that is, d {\displaystyle d} d). Remember that factors are the numbers that can multiply together to make another number. For example, since you can make 6 by multiplying 6 × 1 {\displaystyle 6\times 1} 6\times 1 and 2 × 3 {\displaystyle 2\times 3} 2\times 3, that means 1, 2, 3, and 6 are the factors of 6. In the sample problem, a = 2 {\displaystyle a=2} a=2 and d = 6 {\displaystyle d=6} d=6. The factors of 2 are 1 and 2. The factors of 6 are 1, 2, 3, and 6.
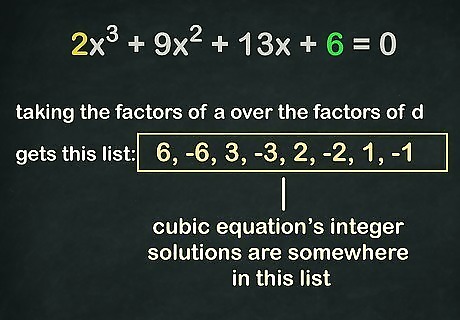
Divide the factors of d {\displaystyle d} d by the factors of a {\displaystyle a} a. Make a list of the values you get by dividing each factor of d {\displaystyle d} d by each factor of a {\displaystyle a} a. This will usually result in lots of fractions and a few whole numbers. The integer solutions to your cubic equation will either be one of the whole numbers in this list or the negative of one of these numbers. In the sample equation, taking the factors of d {\displaystyle d} d (1, 2, 3 and 6) over the factors of a {\displaystyle a} a (1 and 2) gives this list: 6 {\displaystyle 6} 6, − 6 {\displaystyle -6} -6, 3 {\displaystyle 3} 3, − 3 {\displaystyle -3} -3, 2 {\displaystyle 2} {\displaystyle 2}, − 2 {\displaystyle -2} -2, 1 {\displaystyle 1} 1 and − 1 {\displaystyle -1} -1. Your cubic equation's solutions are somewhere in this list.
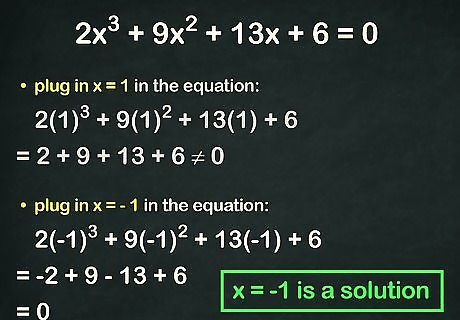
Plug in the integers manually for a simpler but possibly time-consuming approach. Once you have your list of values, you can find the integer answers to your cubic equation by quickly plugging each integer in manually and finding which ones equal 0 {\displaystyle 0} {\displaystyle 0}. For instance, if you plug in 1 {\displaystyle 1} 1, you get: 2 ( 1 ) 3 + 9 ( 1 ) 2 + 13 ( 1 ) + 6 {\displaystyle 2(1)^{3}+9(1)^{2}+13(1)+6} 2(1)^{3}+9(1)^{2}+13(1)+6, or 2 + 9 + 13 + 6 {\displaystyle 2+9+13+6} 2+9+13+6, which clearly does not equal 0 {\displaystyle 0} {\displaystyle 0}. So, move on to the next value on your list. If you plug in − 1 {\displaystyle -1} -1, you get ( − 2 ) + 9 + ( − 13 ) + 6 {\displaystyle (-2)+9+(-13)+6} (-2)+9+(-13)+6, which does equal 0 {\displaystyle 0} {\displaystyle 0}. This means − 1 {\displaystyle -1} -1 is one of your integer solutions.

Employ synthetic division for a more complex but likely faster approach. If you don't want to spend the time plugging in values one by one, try a quicker method that involves a technique called synthetic division. Basically, you'll want to synthetically divide your integer values by the original a {\displaystyle a} a, b {\displaystyle b} b, c {\displaystyle c} c, and d {\displaystyle d} d coefficients in your cubic equation. If you get a remainder of 0 {\displaystyle 0} {\displaystyle 0}, your value is one of the cubic equation's answers. Synthetic division is a complex topic that’s beyond the scope of describing fully here. However, here's a sample of how to find one of the solutions to your cubic equation with synthetic division: -1 | 2 9 13 6 __| -2-7-6 __| 2 7 6 0 Since you got a final remainder of 0 {\displaystyle 0} {\displaystyle 0}, you know that one of your cubic's integer solutions is − 1 {\displaystyle -1} -1.
Using a Discriminant Approach
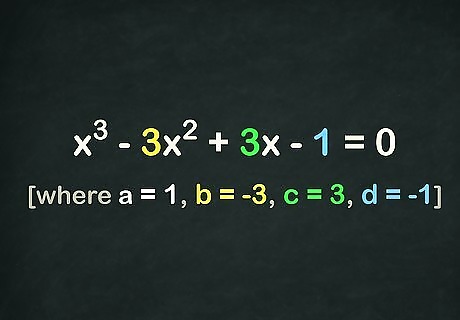
Write out the values of a {\displaystyle a} a, b {\displaystyle b} b, c {\displaystyle c} c, and d {\displaystyle d} d. For this method you’ll be dealing heavily with the coefficients of the terms in your equation. Record your a {\displaystyle a} a, b {\displaystyle b} b, c {\displaystyle c} c, and d {\displaystyle d} d terms before you begin so you don't forget what each one is. For the sample equation x 3 − 3 x 2 + 3 x − 1 {\displaystyle x^{3}-3x^{2}+3x-1} x^{3}-3x^{2}+3x-1, write a = 1 {\displaystyle a=1} a=1, b = − 3 {\displaystyle b=-3} b=-3, c = 3 {\displaystyle c=3} c=3, and d = − 1 {\displaystyle d=-1} d=-1. Don't forget that when an x {\displaystyle x} x variable doesn't have a coefficient, it's implicitly assumed that its coefficient is 1 {\displaystyle 1} 1.
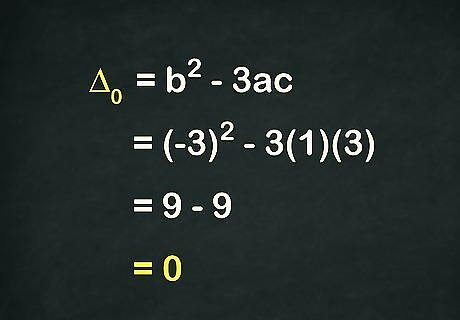
Calculate the discriminant of zero using the proper formula. The discriminant approach to finding a cubic equation's solution requires some complicated math, but if you follow the process carefully, you'll find that it's an invaluable tool for figuring out those cubic equations that are hard to crack any other way. To start, find Δ 0 {\displaystyle \Delta _{0}} \Delta _{0} (the discriminant of zero), the first of several important quantities we'll need, by plugging the appropriate values into the formula Δ 0 = b 2 − 3 a c {\displaystyle \Delta _{0}=b^{2}-3ac} \Delta _{0}=b^{2}-3ac. A discriminant is simply a number that gives us information about the roots of a polynomial (you may already know the quadratic discriminant: b 2 − 4 a c {\displaystyle b^{2}-4ac} b^{2}-4ac). In your sample problem, solve as follows: b 2 − 3 a c {\displaystyle b^{2}-3ac} b^{2}-3ac ( − 3 ) 2 − 3 ( 1 ) ( 3 ) {\displaystyle (-3)^{2}-3(1)(3)} (-3)^{2}-3(1)(3) 9 − 3 ( 1 ) ( 3 ) {\displaystyle 9-3(1)(3)} 9-3(1)(3) 9 − 9 = 0 = Δ 0 {\displaystyle 9-9=0=\Delta _{0}} 9-9=0=\Delta _{0}

Follow up by calculating Δ 1 = 2 b 3 − 9 a b c + 27 a 2 d {\displaystyle \Delta _{1}=2b^{3}-9abc+27a^{2}d} \Delta _{1}=2b^{3}-9abc+27a^{2}d. The next important quantity you’ll need, Δ 1 {\displaystyle \Delta _{1}} \Delta _{1} (the discriminant of 1 {\displaystyle 1} 1), requires a little more work, but is found in essentially the same way as Δ 0 {\displaystyle \Delta _{0}} \Delta _{0}. Plug the appropriate values into the formula 2 b 3 − 9 a b c + 27 a 2 d {\displaystyle 2b^{3}-9abc+27a^{2}d} 2b^{3}-9abc+27a^{2}d to get your value for Δ 1 {\displaystyle \Delta _{1}} \Delta _{1}. In the example, solve as follows: 2 ( − 3 ) 3 − 9 ( 1 ) ( − 3 ) ( 3 ) + 27 ( 1 ) 2 ( − 1 ) {\displaystyle 2(-3)^{3}-9(1)(-3)(3)+27(1)^{2}(-1)} 2(-3)^{3}-9(1)(-3)(3)+27(1)^{2}(-1) 2 ( − 27 ) − 9 ( − 9 ) + 27 ( − 1 ) {\displaystyle 2(-27)-9(-9)+27(-1)} 2(-27)-9(-9)+27(-1) − 54 + 81 − 27 {\displaystyle -54+81-27} -54+81-27 81 − 81 = 0 = Δ 1 {\displaystyle 81-81=0=\Delta _{1}} 81-81=0=\Delta _{1}
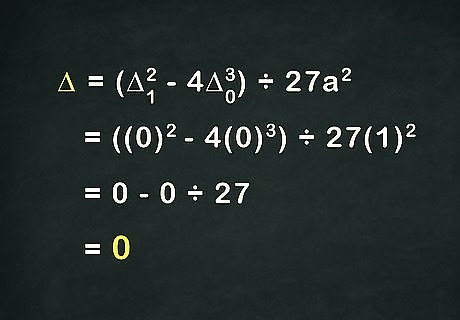
Calculate: Δ = ( Δ 1 2 − 4 Δ 0 3 ) ÷ − 27 a 2 {\displaystyle \Delta =(\Delta _{1}^{2}-4\Delta _{0}^{3})\div -27a^{2}} \Delta =(\Delta _{1}^{2}-4\Delta _{0}^{3})\div -27a^{2}. Next, we'll calculate the discriminant of the cubic from the values of Δ 0 {\displaystyle \Delta _{0}} \Delta _{0} and Δ 1 {\displaystyle \Delta _{1}} \Delta _{1}. In the case of the cubic, if the discriminant is positive, then the equation has three real solutions. If the discriminant is zero, then the equation has either one or two real solutions, and some of those solutions are shared. If it is negative, then the equation has only one solution. A cubic equation always has at least one real solution, because the graph will always cross the x-axis at least once. In the example, since both Δ 0 {\displaystyle \Delta _{0}} \Delta _{0} and Δ 1 {\displaystyle \Delta _{1}} \Delta _{1} = 0 {\displaystyle =0} =0, finding Δ {\displaystyle \Delta } \Delta is relatively easy. Solve as follows: ( Δ 1 2 − 4 Δ 0 3 ) ÷ ( − 27 a 2 ) {\displaystyle (\Delta _{1}^{2}-4\Delta _{0}^{3})\div (-27a^{2})} (\Delta _{1}^{2}-4\Delta _{0}^{3})\div (-27a^{2}) ( ( 0 ) 2 − 4 ( 0 ) 3 ) ÷ ( − 27 ( 1 ) 2 ) {\displaystyle ((0)^{2}-4(0)^{3})\div (-27(1)^{2})} ((0)^{2}-4(0)^{3})\div (-27(1)^{2}) 0 − 0 ÷ 27 {\displaystyle 0-0\div 27} 0-0\div 27 0 = Δ {\displaystyle 0=\Delta } 0=\Delta , so the equation has one or two answers.
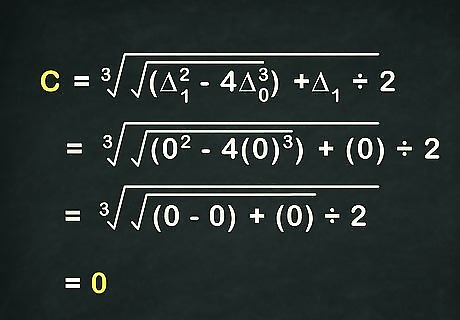
Calculate: C = 3 ( Δ 1 2 − 4 Δ 0 3 + Δ 1 ) ÷ 2 {\displaystyle C=^{3}{\sqrt {\left({\sqrt {\Delta _{1}^{2}-4\Delta _{0}^{3}}}+\Delta _{1}\right)\div 2}}} C=^{3}{\sqrt {\left({\sqrt {\Delta _{1}^{2}-4\Delta _{0}^{3}}}+\Delta _{1}\right)\div 2}}. The last important value we need to calculate is C {\displaystyle C} C. This important quantity will allow us to finally find our three roots. Solve as normal, substituting Δ 1 {\displaystyle \Delta _{1}} \Delta _{1} and Δ 0 {\displaystyle \Delta _{0}} \Delta _{0} as needed. In your example, find C {\displaystyle C} C as follows: 3 ( Δ 1 2 − 4 Δ 0 3 ) + Δ 1 ÷ 2 {\displaystyle ^{3}{\sqrt {{\sqrt {(\Delta _{1}^{2}-4\Delta _{0}^{3})+\Delta _{1}}}\div 2}}} ^{3}{\sqrt {{\sqrt {(\Delta _{1}^{2}-4\Delta _{0}^{3})+\Delta _{1}}}\div 2}} 3 ( 0 2 − 4 ( 0 ) 3 ) + ( 0 ) ÷ 2 {\displaystyle ^{3}{\sqrt {{\sqrt {(0^{2}-4(0)^{3})+(0)}}\div 2}}} ^{3}{\sqrt {{\sqrt {(0^{2}-4(0)^{3})+(0)}}\div 2}} 3 ( 0 − 0 ) + 0 ÷ 2 {\displaystyle ^{3}{\sqrt {{\sqrt {(0-0)+0}}\div 2}}} ^{3}{\sqrt {{\sqrt {(0-0)+0}}\div 2}} 0 = C {\displaystyle 0=C} 0=C

Calculate the three roots with your variables. The roots (answers) to your cubic equation are given by the formula − ( b + u n C + Δ 0 ÷ ( u n C ) ) ÷ 3 a {\displaystyle -(b+u^{n}C+\Delta _{0}\div (u^{n}C))\div 3a} -(b+u^{n}C+\Delta _{0}\div (u^{n}C))\div 3a, where u = ( − 1 + − 3 ) ÷ 2 {\displaystyle u=(-1+{\sqrt {-3}})\div 2} u=(-1+{\sqrt {-3}})\div 2 and n is either 1, 2, or 3. Plug in your values as needed to solve — this requires lots of mathematical legwork, but you should receive three viable answers! You can solve the example by checking the answer when n is equal to 1, 2, and 3. The answers you get from these tests are the possible answers to the cubic equation — any that give an answer of 0 when plugged into the equation are correct. For example, since plugging 1 into x 3 − 3 x 2 + 3 x − 1 {\displaystyle x^{3}-3x^{2}+3x-1} x^{3}-3x^{2}+3x-1 gives an answer of 0, 1 is one of the answers to your cubic equation.



















Comments
0 comment