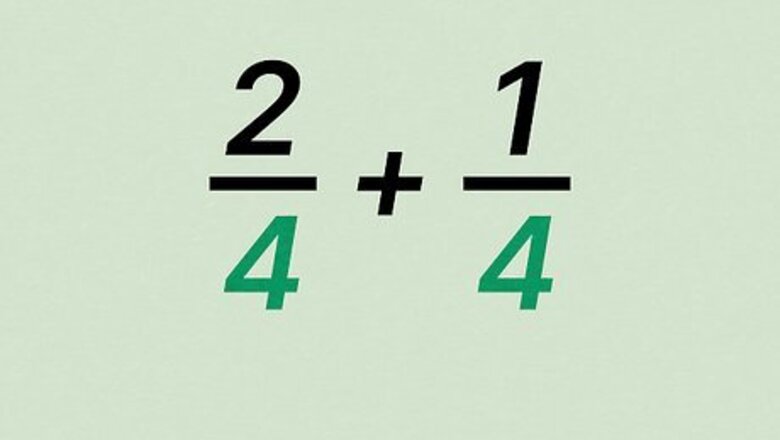
views
Adding Fractions with Like Denominators

Verify the fractions have the same denominator. A denominator is the number below the fraction bar. If the fractions do not have the same denominator, you cannot use this method. For example, if you are calculating 2 4 + 1 4 {\displaystyle {\frac {2}{4}}+{\frac {1}{4}}} {\frac {2}{4}}+{\frac {1}{4}}, you can note that both fractions have the same denominator: 4.
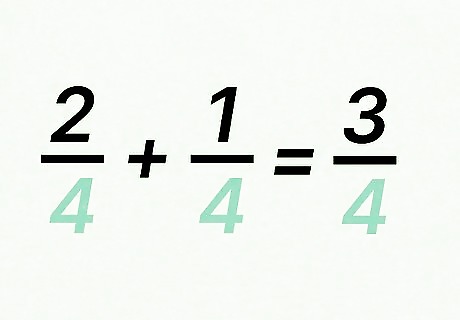
Add the numerators. A numerator is the number above the fraction bar. Add numerators the same way you would add integers. For example, the numerators of 2 4 {\displaystyle {\frac {2}{4}}} {\frac {2}{4}} and 1 4 {\displaystyle {\frac {1}{4}}} {\frac {1}{4}} are 2 and 1, so you would calculate 2 + 1 = 3 {\displaystyle 2+1=3} 2+1=3. So, 3 is the numerator of your sum.
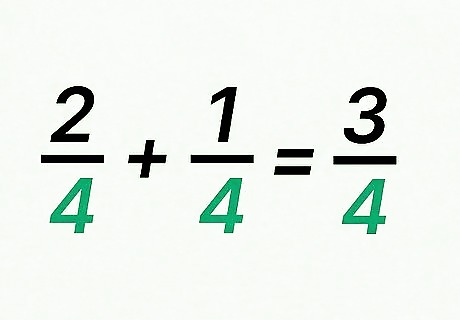
Place the numerators’ sum over the denominator. Since both fractions you are adding have the same denominator, the denominator of their sum will also be the same. For example, the sum of 2 4 + 1 4 {\displaystyle {\frac {2}{4}}+{\frac {1}{4}}} {\frac {2}{4}}+{\frac {1}{4}} will have a denominator of 4: 2 4 + 1 4 = 3 4 {\displaystyle {\frac {2}{4}}+{\frac {1}{4}}={\frac {3}{4}}} {\frac {2}{4}}+{\frac {1}{4}}={\frac {3}{4}}.
Adding Fractions with Unlike Denominators
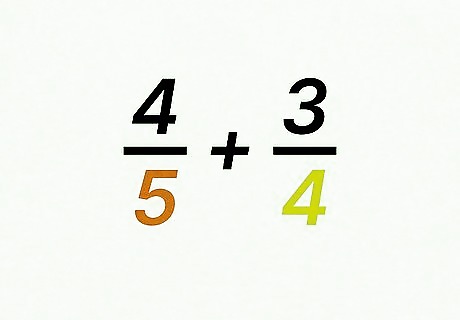
Verify the fractions have different denominators. A denominator is the number below the fraction bar. For example, if you are calculating 4 5 + 3 4 {\displaystyle {\frac {4}{5}}+{\frac {3}{4}}} {\frac {4}{5}}+{\frac {3}{4}}, you can note that the fractions have different denominators: 5 and 4.

List the first several multiples of the smaller denominator. A multiple is a number that another number equally divides into. You can also think of a multiple as the result of multiplying a number by a whole number. You are looking for the smallest multiple that the two denominators have in common. For example, the smallest denominator in 4 5 + 3 4 {\displaystyle {\frac {4}{5}}+{\frac {3}{4}}} {\frac {4}{5}}+{\frac {3}{4}} is 4. The first several multiples of 4 are 4, 8, 12, 16, and 20. The smallest of these multiples that 5 shares with 4 is 20. So, 20 is the least common multiple of the two denominators.
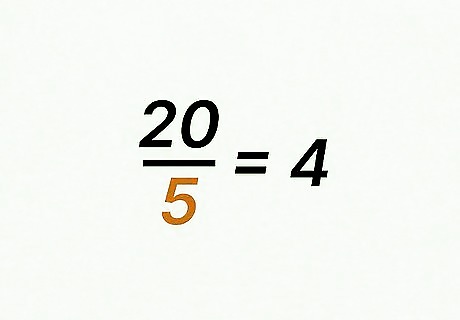
Divide the first fraction’s denominator into the least common multiple. The result will give you a factor of change. This factor tells you how much bigger the common multiple is than the denominator. For example, if the least common multiple is 20, and the first fraction’s denominator is 5, you would calculate 20 5 = 4 {\displaystyle {\frac {20}{5}}=4} {\frac {20}{5}}=4. That means 4 is the factor of change. The least common multiple is 4 times larger than the denominator.
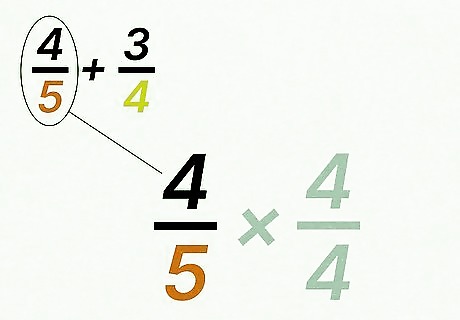
Multiply the numerator of the first fraction by the factor of change. Doing this will keep the numerator and denominator of the equivalent fraction in proportion. For example, if the factor of change is 4, and the first fraction’s numerator is 4, you would calculate 4 × 4 = 16 {\displaystyle 4\times 4=16} 4\times 4=16.
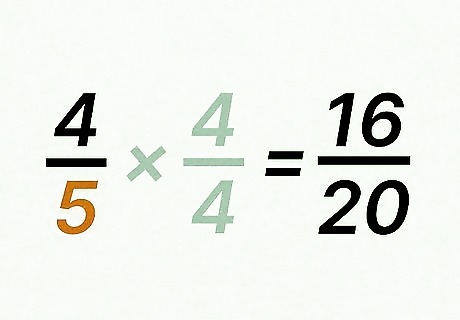
Write the first fraction’s equivalent fraction. The numerator will be the product of the factor of change and the original fraction’s numerator. The denominator will be the least common multiple. For example, 4 5 = 16 20 {\displaystyle {\frac {4}{5}}={\frac {16}{20}}} {\frac {4}{5}}={\frac {16}{20}}.
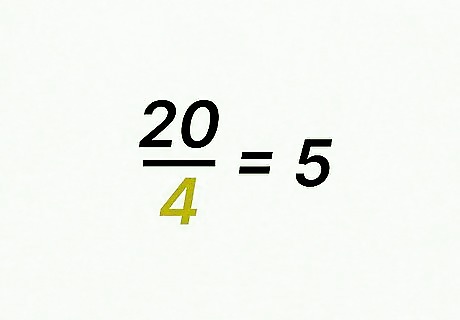
Divide the second fraction’s denominator into the least common multiple. The result will give you a factor of change for the second fraction. This factor tells you how much bigger the common multiple is than the denominator. For example, if the least common multiple is 20, and the second fraction’s denominator is 4, you would calculate 20 4 = 5 {\displaystyle {\frac {20}{4}}=5} {\frac {20}{4}}=5. That means 5 is the factor of change for the second fraction.
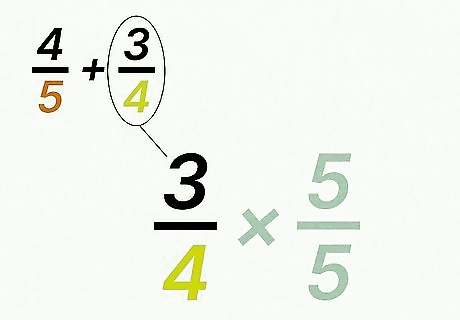
Multiply the numerator of the second fraction by the factor of change. This will give you the numerator of your equivalent fraction. For example, if the factor of change is 5, and the second fraction’s numerator is 3, you would calculate 5 × 3 = 15 {\displaystyle 5\times 3=15} 5\times 3=15.
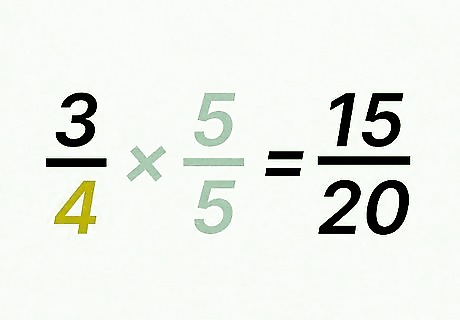
Write the second fraction’s equivalent fraction. The numerator will be the product of the factor of change and the original fraction’s numerator. The denominator will be the least common multiple. For example, 3 4 = 15 20 {\displaystyle {\frac {3}{4}}={\frac {15}{20}}} {\frac {3}{4}}={\frac {15}{20}}.
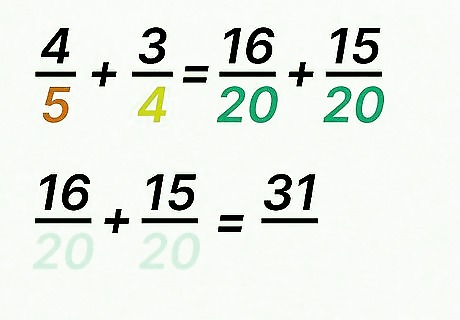
Add the numerators of the equivalent fractions. Since the equivalent fractions have the same denominator, you can add the numerators as you normally would. For example, 16 + 15 = 31 {\displaystyle 16+15=31} 16+15=31.
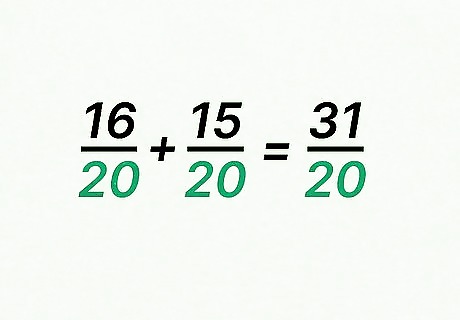
Place the sum of the numerators over the new denominator. Make sure you use the common denominator of the equivalent fractions. For example, 16 20 + 15 20 = 31 20 {\displaystyle {\frac {16}{20}}+{\frac {15}{20}}={\frac {31}{20}}} {\frac {16}{20}}+{\frac {15}{20}}={\frac {31}{20}}.
Simplifying Fractions
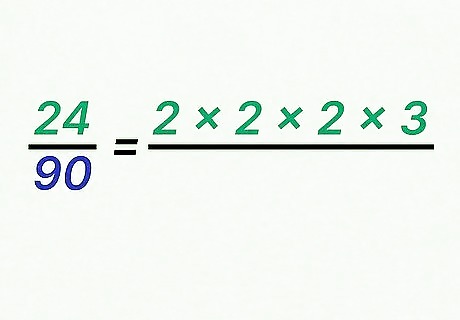
Factor the numerator. You want to factor the numerator into all of its prime factors. Remember that a prime number is a number that is only divisible by 1 and itself. Rewrite the fraction showing this prime factorization in the numerator. For example, if simplifying the fraction 24 90 {\displaystyle {\frac {24}{90}}} {\frac {24}{90}}, you would calculate that 24 = 2 × 2 × 2 × 3 {\displaystyle 24=2\times 2\times 2\times 3} 24=2\times 2\times 2\times 3. So, rewrite the fraction as 2 × 2 × 2 × 3 90 {\displaystyle {\frac {2\times 2\times 2\times 3}{90}}} {\frac {2\times 2\times 2\times 3}{90}}
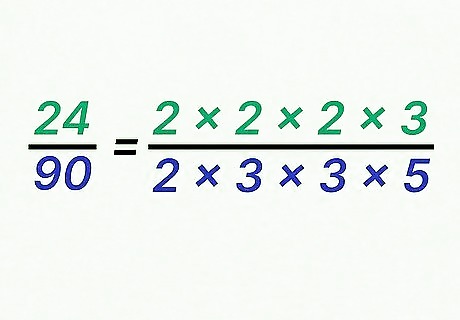
Factor the denominator. You also want to factor the denominator into its prime factors. Rewrite the fraction showing its prime factorization in the denominator. For example, if simplifying the fraction 24 90 {\displaystyle {\frac {24}{90}}} {\frac {24}{90}}, you would calculate that 90 = 2 × 3 × 3 × 5 {\displaystyle 90=2\times 3\times 3\times 5} 90=2\times 3\times 3\times 5. So, rewrite the fraction as 2 × 2 × 2 × 3 2 × 3 × 3 × 5 {\displaystyle {\frac {2\times 2\times 2\times 3}{2\times 3\times 3\times 5}}} {\frac {2\times 2\times 2\times 3}{2\times 3\times 3\times 5}}.
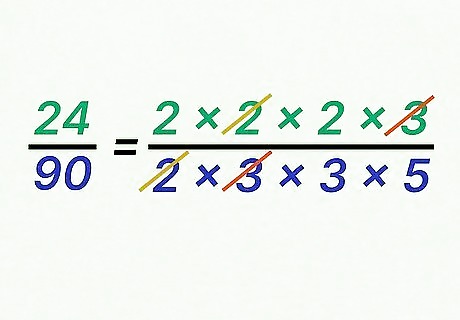
Cancel the factors common to the numerator and denominator. Remember that when a factor is common to the top and bottom of a fraction, it cancels to 1 1 {\displaystyle {\frac {1}{1}}} {\frac {1}{1}}. This means you can eliminate these factors, since any number multiplied by 1 is itself. For example, you can cancel out a 2 and a 3 in the numerator and denominator: 2 × 2 × 2 × 3 2 × 3 × 3 × 5 {\displaystyle {\frac {{\cancel {2\times }}2\times 2{\cancel {\times 3}}}{{\cancel {2\times }}{\cancel {3\times }}3\times 5}}} {\frac {{\cancel {2\times }}2\times 2{\cancel {\times 3}}}{{\cancel {2\times }}{\cancel {3\times }}3\times 5}}. EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher To simplify fractions, you can divide both the numerator and denominator by a common factor. This creates a new, easier-to-use fraction with smaller components, but it represents the same value. For instance, if you divide both the numerator and denominator of 6/12 by 2, you get 3/6, which is equal to 1/2.
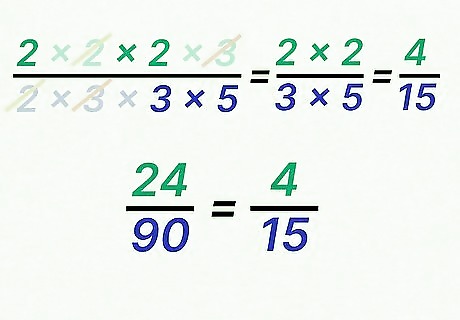
Rewrite the fraction with the remaining factors. You want to simplify the fraction so that it only includes the factors that did not cancel. If more than one factor remains in either the numerator or denominator, you need to multiply them together to get a single integer. The result will be your simplified fraction. For example: 2 × 2 × 2 × 3 2 × 3 × 3 × 5 {\displaystyle {\frac {{\cancel {2\times }}2\times 2{\cancel {\times 3}}}{{\cancel {2\times }}{\cancel {3\times }}3\times 5}}} {\frac {{\cancel {2\times }}2\times 2{\cancel {\times 3}}}{{\cancel {2\times }}{\cancel {3\times }}3\times 5}} 2 × 2 3 × 5 {\displaystyle {\frac {2\times 2}{3\times 5}}} {\frac {2\times 2}{3\times 5}} 4 15 {\displaystyle {\frac {4}{15}}} {\frac {4}{15}}So, the fraction 24 90 {\displaystyle {\frac {24}{90}}} {\frac {24}{90}} simplifies to 4 15 {\displaystyle {\frac {4}{15}}} {\frac {4}{15}}.



















Comments
0 comment