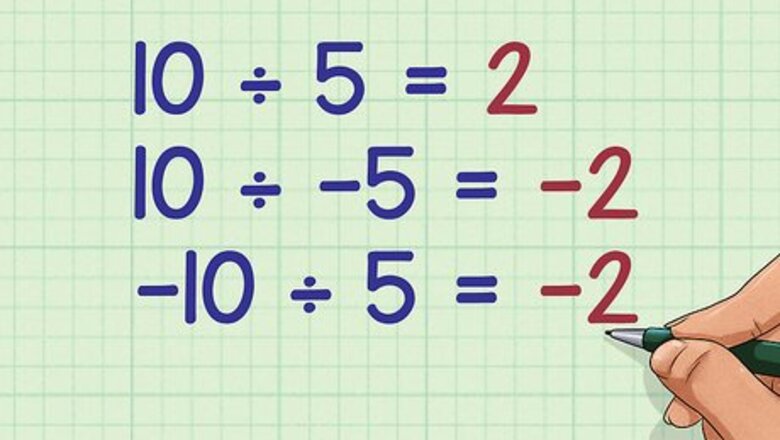
views
Dividing with Negative Numbers
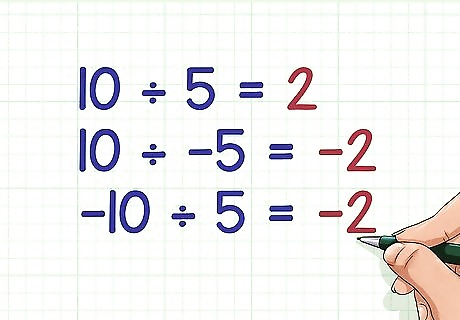
Divide a positive number by a negative number. To do this, divide the integers as usual, then place a negative sign in front of the quotient. A positive number divided by a negative number is always negative. This also is the rule when dividing a negative number by a positive number. For example: 10 ÷ 5 = 2 {\displaystyle 10\div 5=2} 10\div 5=2 10 ÷ − 5 = − 2 {\displaystyle 10\div -5=-2} 10\div -5=-2 − 10 ÷ 5 = − 2 {\displaystyle -10\div 5=-2} -10\div 5=-2
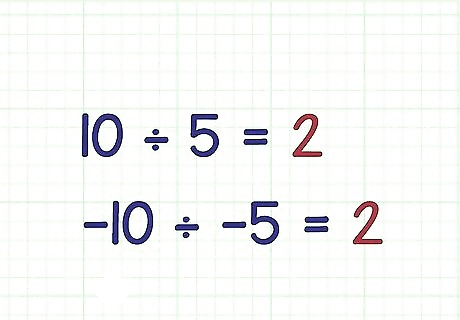
Divide a negative number by a negative number. To do this, divide the integers as usual, and ignore the negative signs. A negative divided by a negative always equals a positive. For example: 10 ÷ 5 = 2 {\displaystyle 10\div 5=2} 10\div 5=2 − 10 ÷ − 5 = 2 {\displaystyle -10\div -5=2} -10\div -5=2
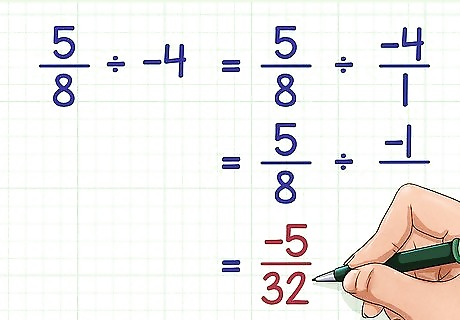
Divide a positive fraction by a negative number. To do this, divide the numbers as usual, then add a negative sign to the quotient. A positive number divided by a negative number will always be negative, regardless of whether the number is a whole number or a fraction. The same is true when dividing a negative number by a positive number. Remember that dividing by a number is the same as multiplying by its reciprocal. For example: 5 8 ÷ − 4 {\displaystyle {\frac {5}{8}}\div -4} {\frac {5}{8}}\div -4 = 5 8 ÷ − 4 1 {\displaystyle ={\frac {5}{8}}\div {\frac {-4}{1}}} ={\frac {5}{8}}\div {\frac {-4}{1}} = 5 8 × − 1 4 {\displaystyle ={\frac {5}{8}}\times {\frac {-1}{4}}} ={\frac {5}{8}}\times {\frac {-1}{4}} = − 5 32 {\displaystyle ={\frac {-5}{32}}} ={\frac {-5}{32}}
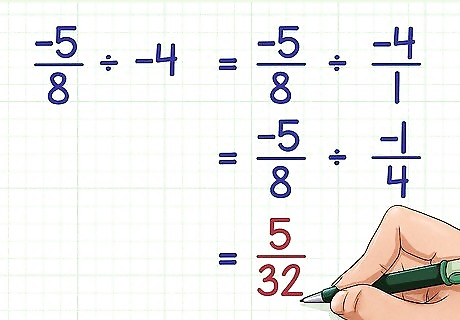
Divide a negative fraction by a negative number. To do this, divide the numbers as usual, and ignore the negative signs. A negative number divided by a negative number will always be positive, regardless of whether the number is a whole number or a fraction. Remember that dividing is the same as multiplying by the reciprocal. For example: − 5 8 ÷ − 4 {\displaystyle {\frac {-5}{8}}\div -4} {\frac {-5}{8}}\div -4 = − 5 8 ÷ − 4 1 {\displaystyle ={\frac {-5}{8}}\div {\frac {-4}{1}}} ={\frac {-5}{8}}\div {\frac {-4}{1}} = − 5 8 × − 1 4 {\displaystyle ={\frac {-5}{8}}\times {\frac {-1}{4}}} ={\frac {-5}{8}}\times {\frac {-1}{4}} = 5 32 {\displaystyle ={\frac {5}{32}}} ={\frac {5}{32}}
Multiplying with Negative Numbers
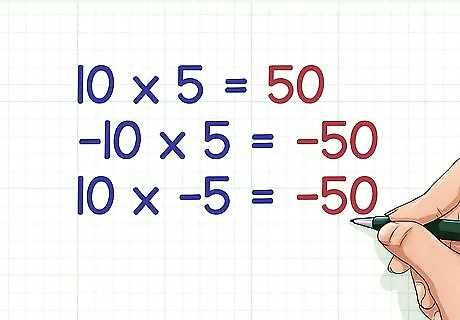
Multiply a positive number by a negative number. To do this, multiply the integers as usual, then add a negative sign to the product. A positive number multiplied by a negative number is always negative. For example: 10 × 5 = 50 {\displaystyle 10\times 5=50} 10\times 5=50 − 10 × 5 = − 50 {\displaystyle -10\times 5=-50} -10\times 5=-50 10 × − 5 = − 50 {\displaystyle 10\times -5=-50} 10\times -5=-50
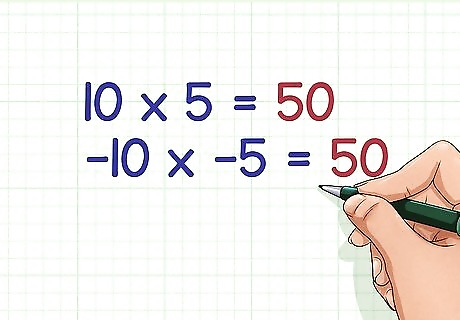
Multiply a negative number by a negative number. To do this, multiply the integers as usual, and ignore the negative signs. A negative number multiplied by a negative number is always positive. For example: 10 × 5 = 50 {\displaystyle 10\times 5=50} 10\times 5=50 − 10 × − 5 = 50 {\displaystyle -10\times -5=50} -10\times -5=50
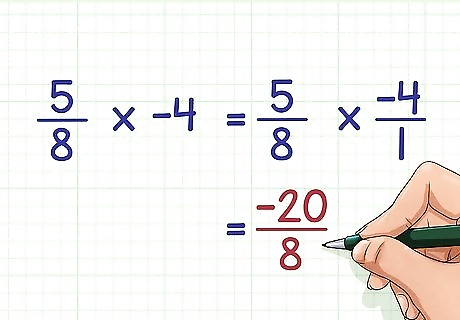
Multiply a positive fraction by a negative number. To do this, multiply the numbers as usual, then add a negative sign to the product. A positive number times a negative number will always be negative, regardless of whether the number is a whole number or a fraction. For example: 5 8 × − 4 {\displaystyle {\frac {5}{8}}\times -4} {\frac {5}{8}}\times -4 = 5 8 × − 4 1 {\displaystyle ={\frac {5}{8}}\times {\frac {-4}{1}}} ={\frac {5}{8}}\times {\frac {-4}{1}} = − 20 8 {\displaystyle ={\frac {-20}{8}}} ={\frac {-20}{8}}
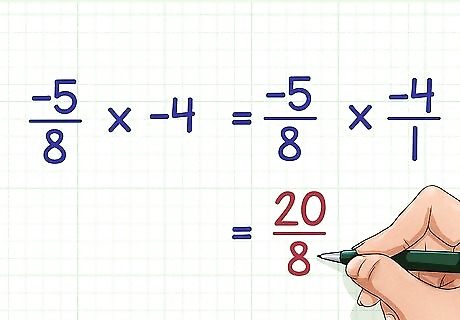
Multiply a negative fraction by a negative number. To do this, multiply the numbers as usual, and ignore the negative signs. A negative number times a negative number will always be positive, regardless of whether the number is a whole number or a fraction. For example: − 5 8 × − 4 {\displaystyle {\frac {-5}{8}}\times -4} {\frac {-5}{8}}\times -4 = − 5 8 × − 4 1 {\displaystyle ={\frac {-5}{8}}\times {\frac {-4}{1}}} ={\frac {-5}{8}}\times {\frac {-4}{1}} = 20 8 {\displaystyle ={\frac {20}{8}}} ={\frac {20}{8}}
Solving Sample Problems
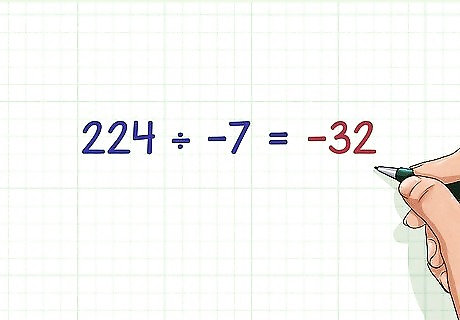
Try this problem. 224 ÷ − 7 {\displaystyle 224\div -7} 224\div -7 Remember that a positive number divided by a negative number will equal a negative number. Since 224 ÷ 7 = 32 {\displaystyle 224\div 7=32} 224\div 7=32, you know that 224 ÷ − 7 = − 32 {\displaystyle 224\div -7=-32} 224\div -7=-32.
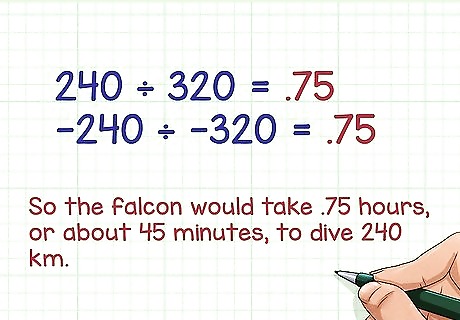
Try this problem. A peregrine falcon can dive (lose height) at a rate of 320 km/hr. Assuming it can sustain this rate indefinitely, how long would it take a peregrine to reach a height of -240 km? Remember that a negative number (-240km) divided by a negative number (-320km/hr) will equal a positive number (number of hours). Since 240 ÷ 320 = .75 {\displaystyle 240\div 320=.75} 240\div 320=.75, you know that − 240 ÷ − 320 = .75 {\displaystyle -240\div -320=.75} -240\div -320=.75. So the falcon would take 0.75 hours, or about 45 minutes, to dive 240 km.
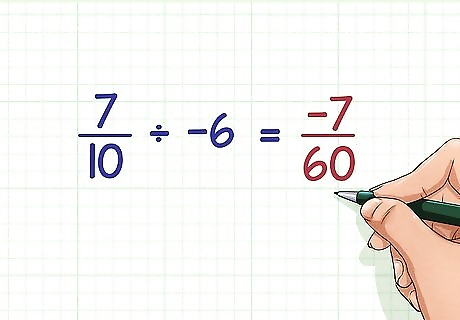
Try this problem. 7 10 ÷ − 6 {\displaystyle {\frac {7}{10}}\div -6} {\frac {7}{10}}\div -6 Remember that a positive fraction divided by a negative number will equal a negative number. Since 7 10 ÷ 6 = 7 10 × 1 6 = 7 60 {\displaystyle {\frac {7}{10}}\div 6={\frac {7}{10}}\times {\frac {1}{6}}={\frac {7}{60}}} {\frac {7}{10}}\div 6={\frac {7}{10}}\times {\frac {1}{6}}={\frac {7}{60}}, you know that 7 10 ÷ − 6 = − 7 60 {\displaystyle {\frac {7}{10}}\div -6={\frac {-7}{60}}} {\frac {7}{10}}\div -6={\frac {-7}{60}}.

Try this problem. − 5 6 ÷ − 3 {\displaystyle {\frac {-5}{6}}\div -3} {\frac {-5}{6}}\div -3 Remember that a negative fraction divided by a negative number will equal a positive number. Since 5 6 ÷ 3 = 5 6 × 1 3 = 5 18 {\displaystyle {\frac {5}{6}}\div 3={\frac {5}{6}}\times {\frac {1}{3}}={\frac {5}{18}}} {\frac {5}{6}}\div 3={\frac {5}{6}}\times {\frac {1}{3}}={\frac {5}{18}}, you know that − 5 6 ÷ − 3 = 5 18 {\displaystyle {\frac {-5}{6}}\div -3={\frac {5}{18}}} {\frac {-5}{6}}\div -3={\frac {5}{18}}.
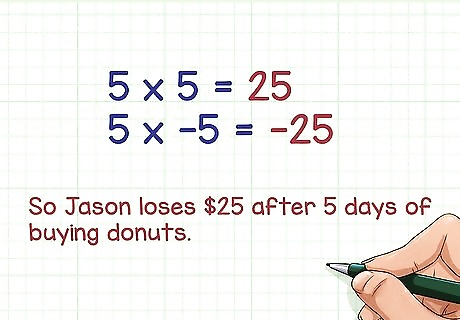
Try this problem. Jason spends 5 dollars on donuts every morning. How much money will he lose on donuts after 5 days? Remember that a positive number (5 days) multiplied by a negative number (-5 dollars) will equal a negative number (money lost). Since 5 × 5 = 25 {\displaystyle 5\times 5=25} 5\times 5=25, you know that 5 × − 5 = − 25 {\displaystyle 5\times -5=-25} 5\times -5=-25. So Jason loses $25 after 5 days of buying donuts.
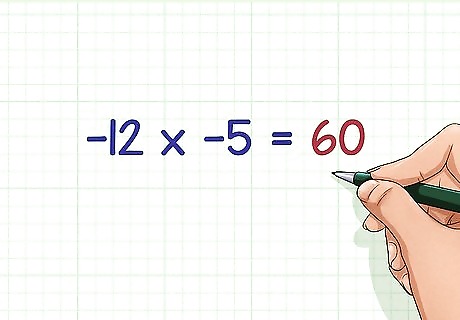
Try this problem. − 12 × − 5 {\displaystyle -12\times -5} -12\times -5 Remember that a negative number times a negative number will always equal a positive number. Since 12 × 5 = 60 {\displaystyle 12\times 5=60} 12\times 5=60, you know that − 12 × − 5 = 60 {\displaystyle -12\times -5=60} -12\times -5=60.
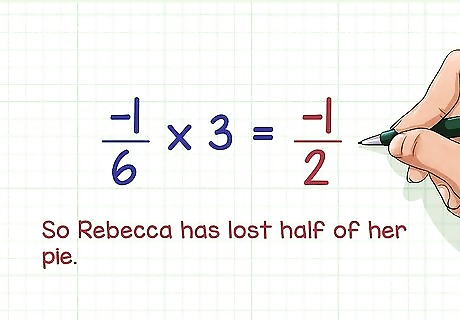
Try this problem. Rebecca has a whole pie in her refrigerator. Over the course of three days, her house guest sneaks into the kitchen and eats 1 6 {\displaystyle {\frac {1}{6}}} {\frac {1}{6}} of the pie. How much pie has Rebecca lost? Remember that a negative fraction ( − 1 6 {\displaystyle {\frac {-1}{6}}} {\frac {-1}{6}} of a pie) times a positive number (3 days), will equal a negative number (amount of pie eaten). Since 1 6 × 3 = 3 6 = 1 2 {\displaystyle {\frac {1}{6}}\times 3={\frac {3}{6}}={\frac {1}{2}}} {\frac {1}{6}}\times 3={\frac {3}{6}}={\frac {1}{2}}, you know that − 1 6 × 3 = − 1 2 {\displaystyle {\frac {-1}{6}}\times 3={\frac {-1}{2}}} {\frac {-1}{6}}\times 3={\frac {-1}{2}}. So Rebecca has lost half of her pie.
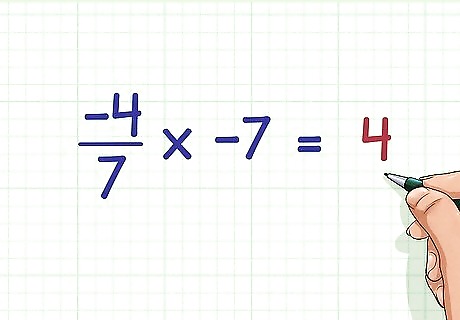
Try this problem. − 4 7 × − 7 {\displaystyle {\frac {-4}{7}}\times -7} {\frac {-4}{7}}\times -7 Remember that a negative fraction times a negative number will equal a positive number. Since 4 7 × 7 = 28 7 = 4 {\displaystyle {\frac {4}{7}}\times 7={\frac {28}{7}}=4} {\frac {4}{7}}\times 7={\frac {28}{7}}=4, you know that − 4 7 × − 7 = 4 {\displaystyle {\frac {-4}{7}}\times -7=4} {\frac {-4}{7}}\times -7=4

















Comments
0 comment