How to Find Normal Force

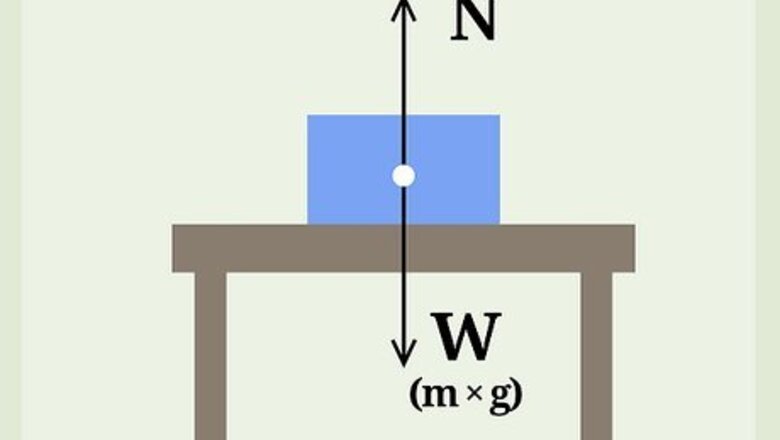
Normal Force at Rest

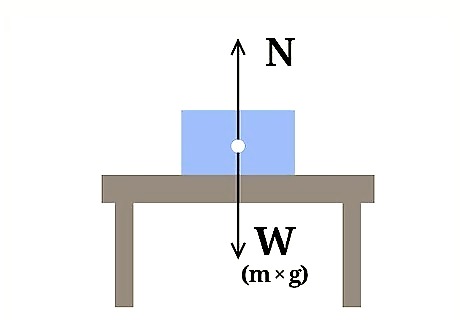
Understand what normal force refers to. Normal force refers to the amount of force use to counteract the force of gravity. Imagine a block sitting on a table. The force of gravity pulls the block toward the Earth, but clearly, there is some force at work preventing the block from crashing through the table and finishing its descent toward the ground. The force responsible for stopping the block in spite of gravitational force is the normal force.

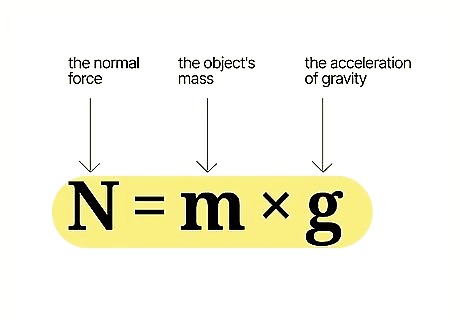
Know the equation for normal force of an object at rest. When calculating an object's normal force when that object is at rest on a flat surface, use the formula: N = m * g In this equation, N refers to the normal force, m refers to the object's mass, and g refers to the acceleration of gravity. For an object sitting on a flat surface, with no outside forces at work, the normal force is equal to the object's weight. In order to keep the object still, the normal force must be equal to the force of gravity at work on the object. The force of gravity at work on the object is that object's weight, or its mass multiplied by the acceleration of gravity. Example: Find the normal force of a block with a mass of 4.2 kg.

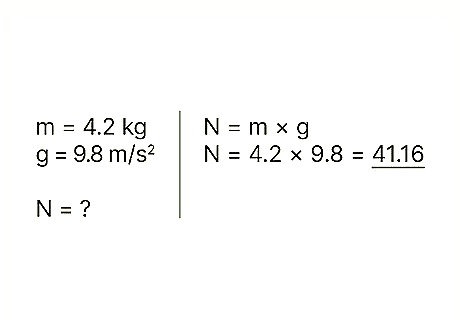
Multiply the object's mass and the acceleration of gravity. Doing so will give you the weight of the object, which ultimately equals the normal force of the object as it sits at rest. Note that the gravitational acceleration at the Earth's surface is a constant: g = 9.8 m/s2 Example: weight = m * g = 4.2 * 9.8 = 41.16

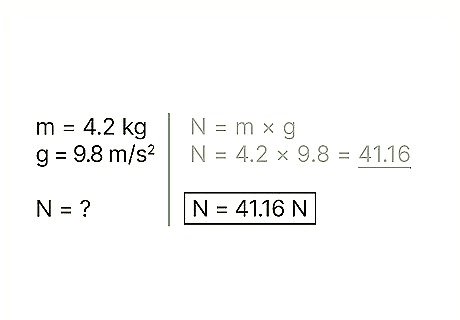
Write down your answer. The previous step should complete the problem, giving you your answer. Example: The normal force is 41.16 N.

Normal Force on an Incline

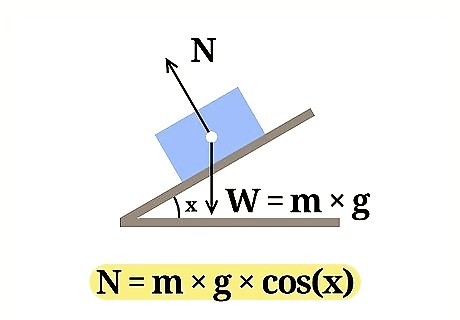
Use the right equation. To calculate the normal force of an object at an angle, you need to use the formula: N = m * g * cos(x) For this equation, N refers to the normal force, m refers to the object's mass, g refers to the acceleration of gravity, and x refers to the angle of incline. Example: Find the normal force of a block with a mass of 4.2 kg, sitting on a ramp with an incline of 45 degrees.

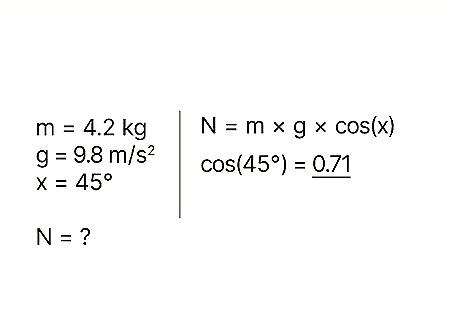
Find the cosine of the angle. The cosign of an angle equals the sine of the complementary angle, or the adjacent side divided by the hypotenuse of the triangle formed by the incline. This value is often determined by a calculator, since the cosine of any angle is constant to that angle, but you can compute it manually, as well. Example: cos (45) = 0.71

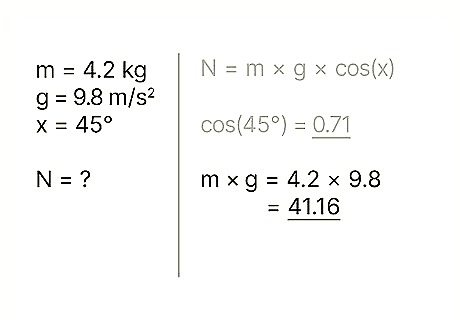
Find the object's weight. The weight of an object equals the mass of the object multiplied by the acceleration of gravity. Note that the gravitational acceleration at the Earth's surface is a constant: g = 9.8 m/s2 Example: weight = m * g = 4.2 * 9.8 = 41.16

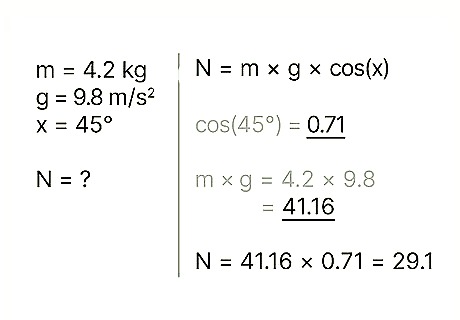
Multiply the two values together. In order to find the normal force, you need to multiply the weight of the object by the cosine of the angle of incline. Example: N = m * g * cos(x) = 41.16 * 0.71 = 29.1

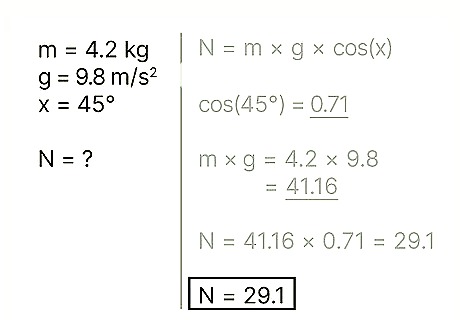
Write your answer. The previous step should complete the problem and give you your answer. Note that for an object sitting on an incline, the normal force should be less than the weight of the object. Example: The normal force is 29.1 N.

Normal Force with an External Downward Force

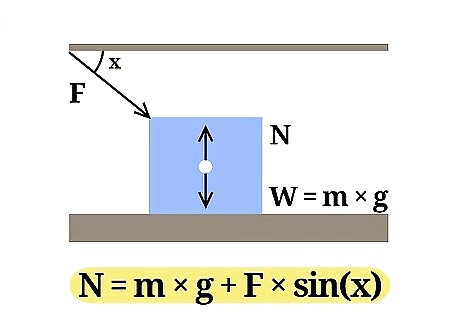
Use the right equation. To calculate the normal force of an object at rest when an outside force acts downward on that object, use the equation: N = m * g + F * sin(x)' N refers to the normal force, m refers to the object's mass, g refers to the acceleration of gravity, F refers to the outside force, and x refers to the angle between the object and the direction of the outside force. Example: Find the normal force of a block with a mass of 4.2 kg, when a person is pressing down on the block at a 30 degree angle with a force of 20.9 N.

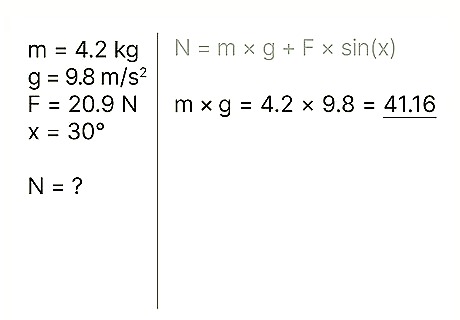
Find the object's weight. The weight of an object equals the mass of the object multiplied by the acceleration of gravity. Note that the gravitational acceleration at the Earth's surface is a constant: g = 9.8 m/s2 Example: weight = m * g = 4.2 * 9.8 = 41.16

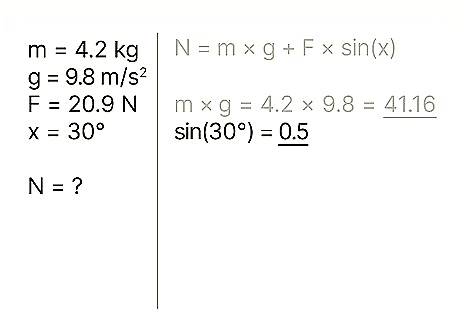
Find the sine of the angle. The sine of an angle is calculated by dividing the side of the triangle opposite the angle by the hypotenuse of the angle. Example: sin(30) = 0.5

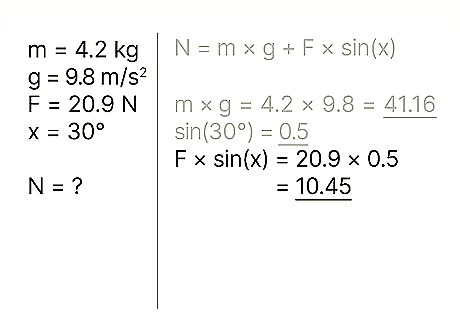
Multiply the sine by the outside force. The outside force, in this instance, refers to the force acting downward on the object. Example: 0.5 * 20.9 = 10.45

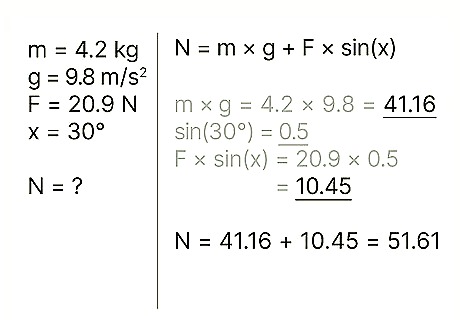
Add this value to the weight. Doing so will give you the normal force at work. Example: 10.45 + 41.16 = 51.61

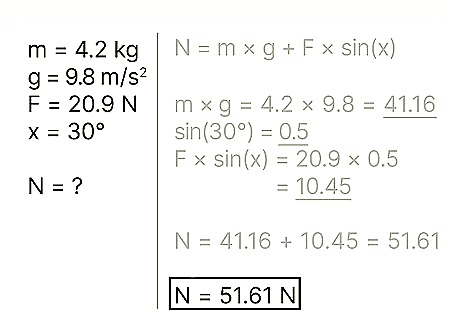
Write your answer. Note that for an object at rest being influenced by an external, downward force, the normal force will be greater than the weight of the object. Example: The normal force is 51.61 N.

Normal Force with an External Upward Force

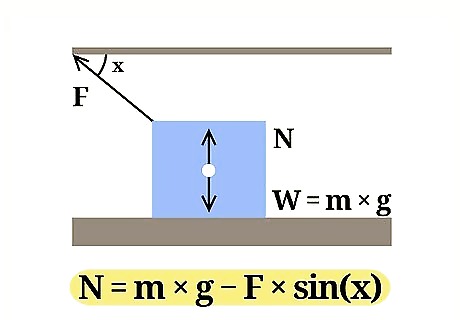
Use the right equation. To calculate the normal force of an object at rest when an outside force acts upward on that object, use the equation: N = m * g - F * sin(x)' N refers to the normal force, m refers to the object's mass, g refers to the acceleration of gravity, F refers to the outside force, and x refers to the angle between the object and the direction of the outside force. Example: Find the normal force of a block with a mass of 4.2 kg, when a person is pulling up at the block at a 50 degree angle with a force of 20.9 N.

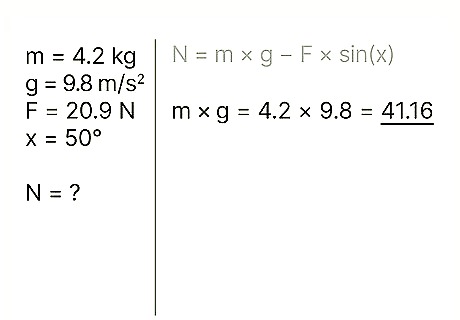
Find the object's weight. The weight of an object equals the mass of the object multiplied by the acceleration of gravity. Note that the gravitational acceleration at the Earth's surface is a constant: g = 9.8 m/s2 Example: weight = m * g = 4.2 * 9.8 = 41.16

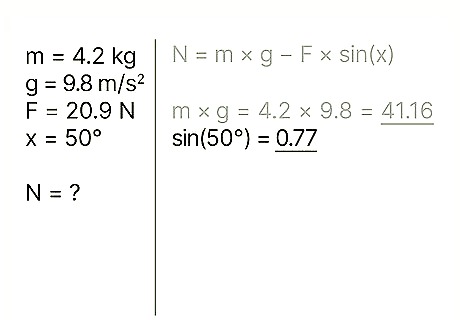
Find the sine of the angle. The sine of an angle is calculated by dividing the side of the triangle opposite the angle by the hypotenuse of the angle. Example: sin(50) = 0.77

Multiply the sine by the outside force. The outside force refers to the force acting upward on the object, in this instance. Example: 0.77 * 20.9 = 16.01

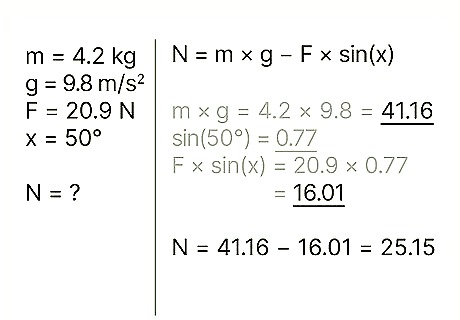
Subtract this value from the weight. Doing so will give you the normal force at work. Example: 41.16 – 16.01 = 25.15

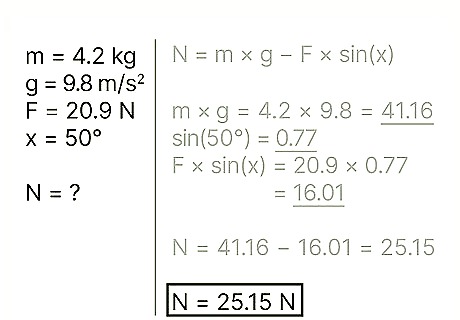
Write your answer. Note that for an object at rest being influenced by an external, upward force, the normal force will be less then the weight of the object. Example: The normal force is 25.15 N.

Normal Force and Friction

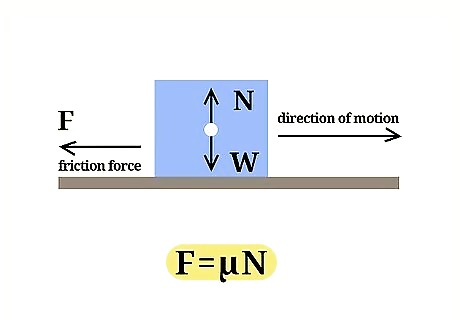
Know the basic equation for kinetic friction. Kinetic friction, or the friction of an object in motion, is equal to the coefficient of friction multiplied by the normal force of an object. In equation format, that looks like: f = μ * N In this equation, f stands for friction, μ refers to the coefficient of friction, and N refers to the normal force of the object. A "coefficient of friction" is the ratio between frictional resistance to normal force, which is responsible for pressing the two opposing surfaces together.

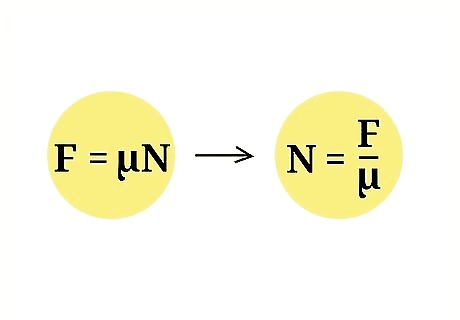
Rearrange the equation to isolate the normal force. If you have a value for the kinetic friction of an object, as well as that object's coefficient of friction, you can calculate the normal force by using the formula: N = f / μ Both sides of the original equation were divided by μ, thereby isolating normal force on one side while accounting for the coefficient of friction and kinetic friction on the opposite side. Example: Find the normal force of a block when the coefficient of friction is 0.4 and the amount of kinetic friction itself is 40 N.

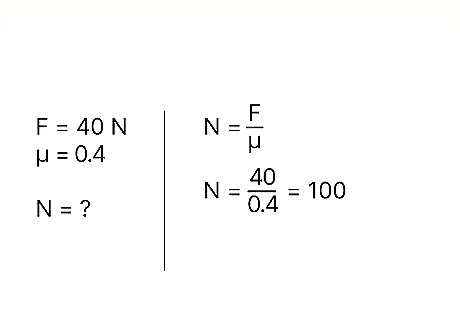
Divide the kinetic friction by the coefficient of friction. This is essentially all you need to do to find the value of the normal force. Example: N = f / μ = 40 / 0.4 = 100

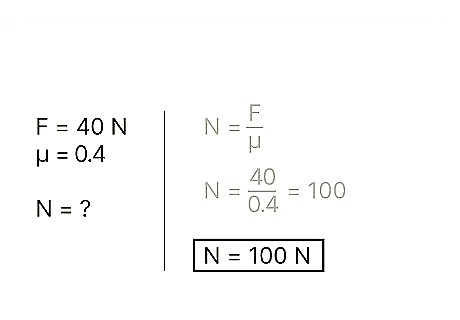
Record your answer. If desired, you can check your answer by plugging it back into the original equation for kinetic friction. Otherwise, you have completed the problem. Example: The normal force is 100.0 N.